Area of an Irregular Quadrilateral Calculator
Area of an Irregular Quadrilateral Calculator: Are you looking for any help while solving the geometry exercises of any class? Then you are on the right place. This page gives the complete details regarding area of an irregular quadrilateral. You can get the information like what is meant by irregular quadrilateral area, formula to calculate the area and simple procedure to solve the irregular quadrilateral questions.
Here are some samples of Area of an Irregular Quadrilateral calculations
- Area of an Irregular Quadrilateral diagonal-e 27 cm diagonal-f 22 cm with angle 2.4 radians
- Area of an Irregular Quadrilateral diagonal-e 29 cm diagonal-f 68 cm with angle 96 degrees
- Area of an Irregular Quadrilateral diagonal-e 75 ft diagonal-f 58 ft with angle 0.7 radians
- Area of an Irregular Quadrilateral diagonal-e 28 ft diagonal-f 75 ft with angle 104 degrees
- Area of an Irregular Quadrilateral diagonal-e 87 in diagonal-f 30 in with angle 85 degrees
- Area of an Irregular Quadrilateral diagonal-e 74 in diagonal-f 50 in with angle 2.1 radians
- Area of an Irregular Quadrilateral diagonal-e 82 m diagonal-f 99 m with angle 2.5 radians
- Area of an Irregular Quadrilateral diagonal-e 84 m diagonal-f 98 m with angle 1.9 radians
- Area of an Irregular Quadrilateral diagonal-e 87 yd diagonal-f 68 yd with angle 138 degrees
- Area of an Irregular Quadrilateral diagonal-e 92 yd diagonal-f 45 yd with angle 122 degrees
- Area of an Irregular Quadrilateral diagonal-e 9 yd diagonal-f 7 ft with angle 2.4 radians
- Area of an Irregular Quadrilateral diagonal-e 2 ft diagonal-f 5 m with angle 96 degrees
- Area of an Irregular Quadrilateral diagonal-e 4 m diagonal-f 3 ft with angle 0.7 radians
- Area of an Irregular Quadrilateral diagonal-e 5 yd diagonal-f 2 cm with angle 104 degrees
- Area of an Irregular Quadrilateral diagonal-e 7 m diagonal-f 6 cm with angle 85 degrees
- Area of an Irregular Quadrilateral diagonal-e 6 m diagonal-f 8 yd with angle 2.1 radians
- Area of an Irregular Quadrilateral diagonal-e 8 yd diagonal-f 4 m with angle 2.5 radians
- Area of an Irregular Quadrilateral diagonal-e 3 ft diagonal-f 9 m with angle 1.9 radians
- Area of an Irregular Quadrilateral diagonal-e 3 in diagonal-f 27 ft with angle 138 degrees
- Area of an Irregular Quadrilateral diagonal-e 2 m diagonal-f 29 ft with angle 122 degrees
- Area of an Irregular Quadrilateral diagonal-e 6 ft diagonal-f 75 cm with angle 1.4 radians
- Area of an Irregular Quadrilateral diagonal-e 4 m diagonal-f 28 yd with angle 158 degrees
- Area of an Irregular Quadrilateral diagonal-e 9 yd diagonal-f 87 cm with angle 2.2 radians
- Area of an Irregular Quadrilateral diagonal-e 8 ft diagonal-f 74 in with angle 2.3 radians
- Area of an Irregular Quadrilateral diagonal-e 5 cm diagonal-f 82 yd with angle 1.1 radians
- Area of an Irregular Quadrilateral diagonal-e 7 in diagonal-f 84 cm with angle 159 degrees
- Area of an Irregular Quadrilateral diagonal-e 4 cm diagonal-f 87 in with angle 47 degrees
- Area of an Irregular Quadrilateral diagonal-e 5 cm diagonal-f 92 yd with angle 3.1 radians
- Area of an Irregular Quadrilateral diagonal-e 7 in diagonal-f 22 ft with angle 118 degrees
- Area of an Irregular Quadrilateral diagonal-e 6 cm diagonal-f 68 yd with angle 18 degrees
- Area of an Irregular Quadrilateral diagonal-e 57 cm diagonal-f 59 in with angle 31 degrees
- Area of an Irregular Quadrilateral diagonal-e 69 cm diagonal-f 67 m with angle 130 degrees
- Area of an Irregular Quadrilateral diagonal-e 30 in diagonal-f 29 m with angle 126 degrees
- Area of an Irregular Quadrilateral diagonal-e 16 m diagonal-f 91 yd with angle 0.8 radians
- Area of an Irregular Quadrilateral diagonal-e 65 in diagonal-f 43 m with angle 1.6 radians
- Area of an Irregular Quadrilateral diagonal-e 40 ft diagonal-f 54 in with angle 0.3 radians
- Area of an Irregular Quadrilateral diagonal-e 61 ft diagonal-f 65 m with angle 0.9 radians
- Area of an Irregular Quadrilateral diagonal-e 41 yd diagonal-f 78 cm with angle 147 degrees
- Area of an Irregular Quadrilateral diagonal-e 66 in diagonal-f 68 ft with angle 2.6 radians
- Area of an Irregular Quadrilateral diagonal-e 16 m diagonal-f 84 cm with angle 100 degrees
Make use of this online tool to get the instant output. Enter the length of two diagonals and angle between the in the input sections and press on the calculate button. Then, the user friendly calculator produces area of the quadrilateral for the given values in fraction of seconds.
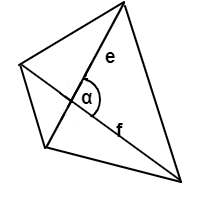
Area of an Irregular Quadrilateral Formula
We are giving some important formulas that helps you to solve the area of an irregular quadrilateral. By having knowledge on the below mentioned formulas, you can easily solve any type of question effortlessly.
1. If diagonals of quadrilateral and angle between them is given,
Area = e * f * sin(α)
Where,
e, f are the lengths of 2 diagonals of a irregular quadrilateral.
α is the angle between angles.
2. If four sides and two opposite angles are given, then
Area = √[(s - a) * (s - b) * (s - c) * (s - d) - a * b * c * d * cos^2(θ/2)]
Where,
a, b, c, d are the sides of a quadrilateral
s = (a + b + c + d) / 2, θ = θ1 + θ2
3. If bimedians and angle between them is given,
Area = m * n * sin(θ)
Where,
m, n are bimedians
θ is the angle between bimedians
How to Find Area of an Irregular Quadrilateral?
Irregular quadrilateral is a quadrilateral where all the sides and angles are not having equal length. Go through the following steps and get the instructions to calculate the irregular quadrilateral area. Make use of of any of these processes and get the answer.
Process 1:
- At first, divide the quadrilateral into two triangles by drawing diagonal that does not disturb the known interior angle.
- Calculate the area of each triangle by using the formula 1/2 * (base) * (height)
- Add areas of those two triangles to obtain the quadrilateral area.
Process 2:
- From the given question, observe the lengths of two diagonals and angle between them.
- Find the sine function of angle.
- Multiply the lengths of diagonals and multiply the product with sin(angle).
- Obtained value is called area of the irregular quadrilateral.
Solved Examples on Irregular Quadrilateral Area
Example 1: In a quadrilateral the diagonal is 42 cm and the two perpendiculars on it from the other vertices are 8 cm and 9 cm respectively. Find the area of the quadrilateral?
Solution:
Given that
AC = 42 cm
BN = 9 cm
DM = 8 cm
Area of ABCD = area of Δ ABC + area of Δ ACD
= ½ * 9 * 42 + ½ * 8 * 42
= 9 * 21 + 4 * 42
= 189 + 168 = 357
∴ Area of Quadrilateral is 357 cm²
Example 2: Find area of irregular quadrilateral? If the length of diagonals is 10 cm, 15 cm with an angle 60 degrees.
Solution:
Given that,
Diagonal length e = 10 cm, f = 15 cm
Angle α = 60 degrees
Area = e * f * sin(α)
Put the values in the formula.
A = 10 * 15 * sin(60)
= 150 * (√3 / 2)
= 129.90
∴ Area of Quadrilateral is 129.90 cm²
Areavolumecalculator.com is an ultimate website and is one stop destination for all kind of geometry problems. You will get the free calculators for any kind of geometry topics on our website.
FAQS on Area of an Irregular Quadrilateral Calculator
1. What is the difference between a regular and an irregular quadrilateral?
Quadrilaterals are of two types, regular and irregular. Regular quadrilateral is a quadrilateral when all the sides are in equal length. Irregular quadrilateral is exactly opposite to the regular one. The examples of regular quadrilateral is square, pentagon, etc. Irregular quadrilateral examples are rectangle, kite, parallelogram.
2. How do you define the area of an irregular quadrilateral?
An irregular quadrilateral is a closed figure having four sides and four angle. The length of all the sides and angle are not same. You must know either the length of all sides or diagonals and angle between the diagonals to find the area of an irregular quadrilateral.
3. What is an example of an irregular quadrilateral?
The some of real time irregular quadrilaterals are trapezoid, rectangle, kite, rhombus, and parallelogram.