Area of an Ellipse Calculator
Area of an Ellipse Calculator: It is a free online calculator tool that generates the accurate output exactly in fraction of seconds. It accepts ellipse of axis a, ellipse of axis b in the given input sections. You have to press the blue color calculate button to obtain the output easily. This Calculator is designed to make your calculations easier by just giving the values in input fields.
Here are some samples of Area of an Ellipse calculations
- Area of an Ellipse a-axis 27 cm b-axis 59 cm
- Area of an Ellipse a-axis 60 cm b-axis 37 cm
- Area of an Ellipse a-axis 65 cm b-axis 32 cm
- Area of an Ellipse a-axis 70 cm b-axis 31 cm
- Area of an Ellipse a-axis 85 ft b-axis 70 ft
- Area of an Ellipse a-axis 55 ft b-axis 91 ft
- Area of an Ellipse a-axis 41 ft b-axis 17 ft
- Area of an Ellipse a-axis 47 ft b-axis 69 ft
- Area of an Ellipse a-axis 84 in b-axis 65 in
- Area of an Ellipse a-axis 86 in b-axis 83 in
- Area of an Ellipse a-axis 7 yd b-axis 3 in
- Area of an Ellipse a-axis 4 m b-axis 2 ft
- Area of an Ellipse a-axis 2 ft b-axis 5 yd
- Area of an Ellipse a-axis 8 yd b-axis 9 cm
- Area of an Ellipse a-axis 6 cm b-axis 6 in
- Area of an Ellipse a-axis 9 yd b-axis 8 m
- Area of an Ellipse a-axis 5 m b-axis 4 in
- Area of an Ellipse a-axis 3 m b-axis 7 cm
- Area of an Ellipse a-axis 7 ft b-axis 27 cm
- Area of an Ellipse a-axis 4 ft b-axis 60 m
- Area of an Ellipse a-axis 2 ft b-axis 65 cm
- Area of an Ellipse a-axis 3 in b-axis 70 m
- Area of an Ellipse a-axis 5 yd b-axis 85 m
- Area of an Ellipse a-axis 8 cm b-axis 55 yd
- Area of an Ellipse a-axis 6 cm b-axis 41 in
- Area of an Ellipse a-axis 9 cm b-axis 47 m
- Area of an Ellipse a-axis 2 ft b-axis 84 in
- Area of an Ellipse a-axis 8 ft b-axis 86 yd
- Area of an Ellipse a-axis 6 cm b-axis 59 in
- Area of an Ellipse a-axis 9 m b-axis 37 ft
- Area of an Ellipse a-axis 11 in b-axis 55 in
- Area of an Ellipse a-axis 26 in b-axis 51 in
- Area of an Ellipse a-axis 99 m b-axis 55 m
- Area of an Ellipse a-axis 55 m b-axis 97 m
- Area of an Ellipse a-axis 21 m b-axis 94 m
- Area of an Ellipse a-axis 35 m b-axis 87 m
- Area of an Ellipse a-axis 87 yd b-axis 17 yd
- Area of an Ellipse a-axis 41 yd b-axis 15 yd
- Area of an Ellipse a-axis 22 yd b-axis 28 yd
- Area of an Ellipse a-axis 21 yd b-axis 94 yd
- Area of an Ellipse a-axis 80 ft b-axis 54 in
- Area of an Ellipse a-axis 64 ft b-axis 56 in
- Area of an Ellipse a-axis 13 ft b-axis 43 m
- Area of an Ellipse a-axis 67 m b-axis 95 yd
- Area of an Ellipse a-axis 87 in b-axis 27 m
- Area of an Ellipse a-axis 56 yd b-axis 23 ft
- Area of an Ellipse a-axis 87 m b-axis 52 in
- Area of an Ellipse a-axis 74 m b-axis 84 in
- Area of an Ellipse a-axis 23 in b-axis 61 cm
- Area of an Ellipse a-axis 37 in b-axis 57 ft
- Area of an Ellipse a-axis 66 yd b-axis 66 m
- Area of an Ellipse a-axis 69 ft b-axis 92 in
- Area of an Ellipse a-axis 79 m b-axis 46 yd
- Area of an Ellipse a-axis 75 ft b-axis 19 m
- Area of an Ellipse a-axis 38 cm b-axis 71 in
- Area of an Ellipse a-axis 34 cm b-axis 57 m
- Area of an Ellipse a-axis 60 yd b-axis 86 in
- Area of an Ellipse a-axis 39 yd b-axis 51 ft
- Area of an Ellipse a-axis 37 ft b-axis 39 m
- Area of an Ellipse a-axis 31 yd b-axis 14 m
Below we will explain how to find the area of an ellipse by hand, what is meant by area of an ellipse and its formula. For those willing to learn the concept can check the following sections to get a clear idea on it.
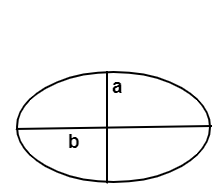
What is the Formula for Area of an Ellipse?
Area of an ellipse is the multiplication of its axis with π. So, to calculate the area of an ellipse, we must have to measure the two axis radius of ellipse. Ellipse area is generally measured in square units. Area of an ellipse is defined as the area covered by all the points of an ellipse. The formula to calculate ellipse area is given by
Area of an ellipse = π (a * b)
Where, a is the major axis radius
b is the minor axis radius
π is a constant which is 22/7 or 3.14
Steps to Find Ellipse Area
You can calculate the area of an ellipse by using the parameters. We tried explaining it in a clear way by taking enough worked out examples. Have a glance at them and know the method approached to arrive at the solution.
- Firstly, figure out the axis of an ellipse from the given question.
- Multiply those axis values.
- Multiply the product with π value.
- Result is area of an ellipse for sure.
Area of an Ellipse Example Problems
Example 1: The ellipse has horizontal radius 16 cm and vertical radius 9 cm. Find the area of ellipse?
Solution:
Given that,
Horizontal radius (a) = 16 cm
Vertical radius (b) = 9 cm
Area = π · a · b
Substitute the values
Area = π · 16 · 9
= 144 π
= 144 * 22 / 7
= 452.57
∴ Area of ellipse is 452.57 cm².
Example 2: Calculate the area of the ellipse where the major radius is 4 cm and minor radius is 3 cm?
Solution:
Given that,
Major axis a = 4 cm
Minor axis b = 3 cm
Area = π · a · b
= π. 4 . 3
= 12 π
= 12 * 3.14
= 37.68
∴ Area of ellipse is 37.68 cm².
Explore more mathematical concepts from our site Areavolumecalculator.com by using our free online geometry calculators and make your calculations easy during homework.
FAQs on Ellipse Area Calculator
1. What are the applications of Ellipse?
We have wide applications in the field of physics, engineering, etc. For example, all the plants revolve in their orbits which are elliptical. Astronomy has a lot of use of this shape as many of the stars and plants are in elliptical shape.
2. How do you define ellipse?
Ellipse is a curve on the plane which is in oval shape. The sum of distances to its two focal points is always a constant quantity from any points on the elliptical curve. It belongs to the family of circles with both focal points at the same location. If major and minor axis in the ellipse are of same length and both foci at the center, then it becomes a circle.
3. How do you find the area of an ellipse?
You can use this free calculator tool to find the area of an ellipse easily. Or get the help from the manual procedure mentioned on this page to check the area of an ellipse.
4. Find the area of an ellipse. If diameter of major axis is 20 cm, minor axis is 14 cm.
Diameter of major axis d1 = 20 cm
Diameter of minor axis d2 = 14 cm
Area of an ellipse = π / 4 (d1 * d2)
Area = π / 4 (20 * 14) = π * 10 * 7
Area of an ellipse = 70π