Area of Sector Calculator
Area of a Sector Calculator: Actually, it is very tough to remember all the formulas in the geometry class. You need not worry as we are here to help you out with this problem. This handy tool displays the sector area of a circle within seconds. Just few taps are required to find the area using our online calculator. So, why to search for other resources, simply enter radius, angle at the specified input sections and press on the calculate button.
Here are some samples of Area of a Sector calculations
In this page, you can find what are the steps to calculate the area of a sector, its formula, and solved example sections.
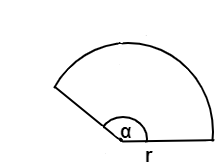
Area of a Sector of a Circle Formula
The area of a sector is basically defined as the number of square units required exactly to fill the sector of a circle. The formula to find those square units is listed here
If angle is in radians,
Area of a sector a = r² * α / 2
If angle is in degrees, then
Area a = (α) / (360°) * πr²
Where, r is the radius of the circle
α is the angle between the radius and sector
Manual Process to Find Area of a Sector
Below are some guidelines which are useful for you to evaluate the area of a sector of circle effortlessly. Check out the instructions and follow them carefully to get the exact answer.
- Read the question attentively and make a note of the radius and angle.
- Do half of the angle value which is in radians or degrees.
- Square the given radius value and multiply the obtained value with the half of angle.
- Finally outcome is the exact sector area.
Area of a Sector Solved Examples
Example 1: Find the area of a section with radius 4 m and angle 45°?
Solution:
Given that,
Radius r = 4 m
Angle α = 45°
Area of sector = (α) / (360°) * πr²
= (45°) / (360°) * π * 4²
= 0.125 * 3.14 * 4 * 4
= 6.28
∴ Area of sector is 6.28 m²
Example 2: A sector with an area 48π cm² has radius of 16 cm. What is the central angle measure of the sector in radians?
Solution:
Given that,
Area of sector a = 48π cm²
radius r = 16 cm
Area of a sector = r² * α / 2
48π = 16² * α / 2
48π * 2 = 16 * 16 * α
96π = 256 * α
α = 256 / 96π
= (256 * 7) / (96 * 22) = 1792 / 2112
= 0.848 or 3π / 8
FAQS on Area of a Sector Calculator
1. What is the formula for area of a sector?
Sector area = (πr²) × (central angle in degrees / 360°). If the central angle is measured in radians.
Sector area = r² × (central angle in radians / 2). If the central angle is measured in degrees.
2. If the length of the arc of a circle with radius 16 units is 5 units, the area of the sector corresponding to that arc?
Area = (l * r) / 2
= (16 * 5) / 2
= 8 * 5 = 40 square units
3. What are the examples of sector area?
The real time examples of a sector area is slice of a cake piece separated from the birthday party cake. From the whole pizza, a part of the pizza separated from the original one, others.
4. Where can I get the best tools to find the sector area of a circle?
You can get the best online tools for calculating the sector area of an circle at trusted and genuine website Areavolumecalculator.com
