Area of a Triangle Calculator

Created By : Abhinandan Kumar

Reviewed By : Rajashekhar Valipishetty

Last Updated : May 01, 2023

Area of Triangle -The area of a triangle is defined as the total space that is enclosed by any particular triangle. The basic formula to find the area of a given triangle is A = 1/2 × b × h, where b is the base and h is the height of the given triangle.

Area of a Triangle Calculator: The Triangle Area Calculator provided here helps you determine the Area of Triangle easily. You can find the area of triangle without any hassle by simply providing the base and height metrics in the input field. You will get the corresponding Area of Triangle thereafter in a fraction of seconds. Make your calculations much easier and faster with our handy calculator.

Get to know further information on What is Area of Triangle and how to calculate Area of Triangle using different methods.

Area of a Triangle Calculator

Area of a Triangle Calculator (SSS)

Area of a Triangle Calculator(SSS)

Enter the Base (a)

Enter the Base (b)

Enter the Base (c)


Here are some samples of Area of a Triangle calculations(SSS)

  • Area of a Triangle 78 cm by 44 cm by 90 cm
  • Area of a Triangle 67 cm by 87 cm by 92 cm
  • Area of a Triangle 44 ft by 33 ft by 64 ft
  • Area of a Triangle 89 ft by 65 ft by 99 ft
  • Area of a Triangle 35 in by 64 in by 83 in
  • Area of a Triangle 41 in by 36 in by 64 in
  • Area of a Triangle 31 m by 50 m by 70 m
  • Area of a Triangle 58 m by 55 m by 87 m
  • Area of a Triangle 62 yd by 64 yd by 37 yd
  • Area of a Triangle 53 yd by 46 yd by 23 yd
  • Area of a Triangle 9 m by 6 m by 8 yd
  • Area of a Triangle 5 in by 5 in by 4 cm
  • Area of a Triangle 8 m by 6 yd by 5 yd
  • Area of a Triangle 9 ft by 5 yd by 7 m
  • Area of a Triangle 4 yd by 7 yd by 4 m
  • Area of a Triangle 7 ft by 9 m by 7 m
  • Area of a Triangle 4 yd by 4 yd by 9 ft
  • Area of a Triangle 5 yd by 6 yd by 4 ft
  • Area of a Triangle 99 in by 3 m by 23 in
  • Area of a Triangle 93 in by 4 yd by 59 in
  • Area of a Triangle 60 in by 2 yd by 95 cm
  • Area of a Triangle 73 ft by 6 m by 65 ft
  • Area of a Triangle 64 yd by 7 m by 62 yd
  • Area of a Triangle 76 cm by 6 m by 21 ft
  • Area of a Triangle 41 yd by 8 m by 31 m
  • Area of a Triangle 31 cm by 8 ft by 98 in
  • Area of a Triangle 98 ft by 6 yd by 91 ft
  • Area of a Triangle 63 in by 8 yd by 21 ft
  • Area of a Triangle 39 cm by 3 in by 36 cm
  • Area of a Triangle 68 cm by 7 in by 68 cm
  • Area of a Triangle 47 m by 95 ft by 69 ft
  • Area of a Triangle 20 yd by 93 m by 83 m
  • Area of a Triangle 43 ft by 14 m by 49 ft
  • Area of a Triangle 89 ft by 65 in by 29 yd
  • Area of a Triangle 54 yd by 58 yd by 48 ft
  • Area of a Triangle 13 m by 37 ft by 15 ft
  • Area of a Triangle 36 m by 34 yd by 55 ft
  • Area of a Triangle 86 ft by 71 ft by 34 m
  • Area of a Triangle 31 ft by 82 m by 84 m
  • Area of a Triangle 58 m by 69 yd by 69 ft
  • Area of a Triangle 24 m by 14 ft by 25 yd
  • Area of a Triangle 60 yd by 70 m by 58 yd
  • Area of a Triangle 94 cm by 51 in by 61 in
  • Area of a Triangle 37 in by 35 in by 80 cm
  • Area of a Triangle 79 ft by 25 yd by 19 m
  • Area of a Triangle 77 m by 89 yd by 58 ft
  • Area of a Triangle 53 ft by 53 m by 72 yd
  • Area of a Triangle 77 in by 58 cm by 70 in
  • Area of a Triangle 21 ft by 35 yd by 97 ft
  • Area of a Triangle 22 yd by 85 yd by 92 m

    • Area of a Triangle Calculator (SSA)

    Area of a Triangle Calculator(SSA)

    Enter the Side (a)

    Enter the Side (b)

    Enter the Angle (γ)



    Here are some samples of Area of a Triangle calculations(SSA)

  • Area of a Triangle 60 cm by 80 cm with angle 67 degrees
  • Area of a Triangle 22 cm by 47 cm with angle 6 degrees
  • Area of a Triangle 71 ft by 27 ft with angle 0.4 radians
  • Area of a Triangle 81 ft by 25 ft with angle 4 degrees
  • Area of a Triangle 45 in by 88 in with angle 0.7 radians
  • Area of a Triangle 83 in by 92 in with angle 0.5 radians
  • Area of a Triangle 73 m by 73 m with angle 146 degrees
  • Area of a Triangle 93 m by 44 m with angle 1.5 radians
  • Area of a Triangle 29 yd by 14 yd with angle 2.9 radians
  • Area of a Triangle 11 yd by 61 yd with angle 0.3 radians
  • Area of a Triangle 4 m by 9 cm with angle 67 degrees
  • Area of a Triangle 6 in by 4 yd with angle 6 degrees
  • Area of a Triangle 5 cm by 5 ft with angle 0.4 radians
  • Area of a Triangle 9 cm by 7 in with angle 4 degrees
  • Area of a Triangle 8 in by 2 cm with angle 0.7 radians
  • Area of a Triangle 7 in by 3 m with angle 0.5 radians
  • Area of a Triangle 2 in by 6 m with angle 146 degrees
  • Area of a Triangle 3 cm by 8 m with angle 1.5 radians
  • Area of a Triangle 5 in by 60 cm with angle 2.9 radians
  • Area of a Triangle 7 yd by 22 cm with angle 0.3 radians
  • Area of a Triangle 9 in by 71 cm with angle 85 degrees
  • Area of a Triangle 4 yd by 81 ft with angle 0.1 radians
  • Area of a Triangle 3 cm by 45 yd with angle 0.8 radians
  • Area of a Triangle 8 yd by 83 ft with angle 0.9 radians
  • Area of a Triangle 2 ft by 73 in with angle 1.2 radians
  • Area of a Triangle 6 yd by 93 m with angle 104 degrees
  • Area of a Triangle 5 yd by 29 in with angle 102 degrees
  • Area of a Triangle 9 in by 11 ft with angle 151 degrees
  • Area of a Triangle 8 yd by 80 in with angle 1.1 radians
  • Area of a Triangle 7 yd by 47 cm with angle 2.6 radians
  • Area of a Triangle 20 cm by 65 m with angle 2 radians
  • Area of a Triangle 94 cm by 25 m with angle 155 degrees
  • Area of a Triangle 78 ft by 31 in with angle 106 degrees
  • Area of a Triangle 58 ft by 63 m with angle 37 degrees
  • Area of a Triangle 17 yd by 48 ft with angle 20 degrees
  • Area of a Triangle 67 m by 28 ft with angle 102 degrees
  • Area of a Triangle 49 cm by 64 m with angle 1.4 radians
  • Area of a Triangle 86 ft by 39 in with angle 97 degrees
  • Area of a Triangle 64 ft by 75 m with angle 1.3 radians
  • Area of a Triangle 35 ft by 64 yd with angle 13 degrees

    • Area of a Triangle Calculator (ASA)

    Area of a Triangle Calculator(ASA)
    Enter the Angle (β)

    Enter the Base (a)

    Enter the Angle (γ)



    Here are some samples of Area of a Triangle calculations(ASA)

  • Area of a Triangle angle-β 1 radians by 7 ft with angle-γ 118 degrees
  • Area of a Triangle angle-β 0.4 radians by 8 cm with angle-γ 2.7 radians
  • Area of a Triangle angle-β 53 degrees by 9 yd with angle-γ 55 degrees
  • Area of a Triangle angle-β 2.2 radians by 7 m with angle-γ 21 degrees
  • Area of a Triangle angle-β 19 degrees by 4 cm with angle-γ 154 degrees
  • Area of a Triangle angle-β 39 degrees by 2 cm with angle-γ 28 degrees
  • Area of a Triangle angle-β 0.2 radians by 7 cm with angle-γ 1.8 radians
  • Area of a Triangle angle-β 0.9 radians by 3 m with angle-γ 33 degrees
  • Area of a Triangle angle-β 1.7 radians by 9 m with angle-γ 75 degrees
  • Area of a Triangle angle-β 93 degrees by 8 ft with angle-γ 54 degrees
  • Area of a Triangle angle-β 0.8 radians by 6 in with angle-γ 57 degrees
  • Area of a Triangle angle-β 0.6 radians by 6 cm with angle-γ 0.5 radians
  • Area of a Triangle angle-β 0.8 radians by 31 m with angle-γ 2 radians
  • Area of a Triangle angle-β 0.3 radians by 81 yd with angle-γ 130 degrees
  • Area of a Triangle angle-β 0.9 radians by 45 yd with angle-γ 120 degrees
  • Area of a Triangle angle-β 0.5 radians by 56 in with angle-γ 0.8 radians
  • Area of a Triangle angle-β 0.9 radians by 85 cm with angle-γ 94 degrees
  • Area of a Triangle angle-β 44 degrees by 75 yd with angle-γ 16 degrees
  • Area of a Triangle angle-β 0.4 radians by 16 m with angle-γ 2 radians
  • Area of a Triangle angle-β 75 degrees by 74 in with angle-γ 74 degrees
  • Area of a Triangle angle-β 17 degrees by 98 yd with angle-γ 106 degrees
  • Area of a Triangle angle-β 86 degrees by 34 cm with angle-γ 57 degrees
  • Area of a Triangle angle-β 120 degrees by 77 in with angle-γ 1 degrees
  • Area of a Triangle angle-β 1.8 radians by 16 in with angle-γ 47 degrees
  • Area of a Triangle angle-β 0.7 radians by 50 m with angle-γ 4 degrees
  • Area of a Triangle angle-β 40 degrees by 41 cm with angle-γ 124 degrees
  • Area of a Triangle angle-β 1 radians by 29 in with angle-γ 0.9 radians
  • Area of a Triangle angle-β 50 degrees by 87 cm with angle-γ 10 degrees
  • Area of a Triangle angle-β 0.5 radians by 66 yd with angle-γ 99 degrees
  • Area of a Triangle angle-β 2.2 radians by 17 in with angle-γ 0.1 radians

    • What is meant by Area of Triangle?

    The area is defined as the region occupied by the Triangle. Usually, Triangle is a two-dimensional figure that has three edges and three vertices. Depending on the sides and angles triangle can be classified into many types. The most important property of the triangle is that the sum of the interior angles of a triangle is 180 degrees. As triangle is a 2D figure it has both area and perimeter.

    How to find the Area of Triangle?

    Triangle is the most basic shape and almost everyone remembers it right from the school.

      Area of triangle = (1/2)bh Square Units

    Where b is the base of the triangle and h is the height of the triangle.

    However, in certain cases, it is difficult to find the height of the triangle. In such cases, you can use different equations depending on the data you know about the triangle.

    Three Sides(SSS)

    If you know the three sides of a triangle then you can go with Heron's formula i.e.

      Area = √(s * (s - a) * (s - b) * (s - c))

    where "s" is the semi perimeter and is half of the perimeter of the triangle i.e. s = (a + b + c) / 2

    the other way of getting the area is to use the lengths of the triangle itself instead of going with semiperimeter i.e.

      Area = 0.25 * √((a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c))

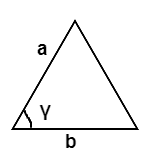
    Two sides and the angle between them (SAS)

    You can find the area of the triangle easily using trigonometric laws when you are given two sides and one angle.

      Area = 0.5 * a * b * sin(γ)

    γ is the angle between the sides a and b.

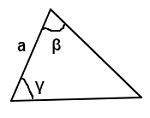
    Two angles and a side between them (ASA)

    You can use this formula when you are given one side and two angles.

      Area = = a² * sin(β) * sin(γ) / (2 * sin(β + γ))

    γ and β are the angles along the given side a.

    Example

    Calculate the area of a triangle if the base and height are 4cm and 5cm respectively?

    Solution:

    The basic formula to find the Area of Triangle = (1/2)bh

    Given Base = 4 Cm

    Height = 5 Cm

    Substitute the given values in the formula and on doing so we will get it as such

    Area of Triangle = (1/2)4*5

    = 0.5*4*5

    = 10 cm2

    How to use the Area of Triangle Calculator?

    Go through the simple and easy steps on how to use the Area of Triangle Calculator. Follow the instructions carefully and arrive at the solution you want.

    • Enter the values of base and height in the input field provided.
    • And then, choose the metric you want to give base and height in cm, m, ft, yd, mi, etc. and click on the Area Button.
    • Finally, the Area of Triangle will be displayed in the output section.

    FAQs on Area of Triangle

    1. What is the formula for finding the area of a triangle?

    The area of the triangle can be found using the formula Area = (1/2)bh.

    2. How do I calculate the Area of a Triangle?

    You can find the area of a triangle using our calculator in a fraction of second.

    3. What is the Area of Triangle for base 5 cm and height 7 cm?

    Area of Triangle = (1/2)bh

    = (1/2)5*7

    = 0.5*5*7

    = = 17.5 Cm2

    4. How to find the area of a triangle given three sides?

    If you are given three sides of a triangle, you can find the area of the triangle using Heron's formula i.e. Area = √(s * (s - a) * (s - b) * (s - c)).