Volume Calculator
Are you looking for a free online calculator that computes the volume of any geometric shape? You are at the right place our handy Volume Calculator will give answers to all your questions in a short span of time. Avail the easy to operate tool to find the volume.
| Volume | ||
Volume Calculator tool is helpful to find the volume of circular cone, capsule, circular cylinder, conical frustum, cube, pyramid, hemisphere, rectangular prism, triangular prism, sphere, box and spherical cap. You must select any one of these geometric shape and provide the required input fields. Hit on the volume button to see the exact results easily & quickly. In addition to the instant output, you can also find the formulas and step by step procedure to solve the volume.
What is meant by Volume?
Volume is the quantity of a three dimensional space enclosed by a closed surface. The space that a substance or shape occupies is also called the volume. The SI unit of volume is cubic meter.
Volume Formulas
The formula involved in finding the volume of a shape is not same. It totally depends on the shape of the substance. Get the formulas for various shapes volume in the following sections.
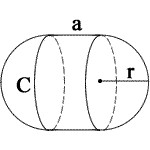
The formula to calculate volume of a Capsule is V = πr²((4/3)r + a)
Circular Cone Volume formula is V = (1/3)πr²h
Conical Frustum Volume is V = (1/3)πh (r₁² + r₂² + (r₁ * r₂))
Circular Cylinder Volume formulas is V = πr²h
Cube Volume formula is V = a3
The formula of Hemisphere Volume is V = (2/3)πr3
Pyramid Volume formula is V = (1/3)a²h
Rectangular Prism volume formula is V = lwh
Sphere Volume formula is V = (4/3)πr3
Spherical Cap Volume formula is V = (1/3)πh²(3R - h)
Triangular Prism Volume formula is V = (1/4)h√[(a + b + c)(b + c -a)(c + a - b)(a + b - c)]
Ellipsoid Volume Formula is V= (4/3)πabc
Volume of a Capsule Formula
Capsule volume, surface area and circumference formulas are given here:
- Volume of a capsule:
- = πr²((4/3)r + a)
- Surface area of a capsule:
- S = 2πr(2r + a)
- Circumference of a capsule:
- C = 2πr
Where,
r is the radius of the circle
a is the side length
Formula to Calculate Circular Cone
Circular cone is a closed figure having circle at the bottom and two lines on the circle joins at one point. Its formulas are here.
- Volume of a Cone:
- V = (1/3)πr²h
- Slant height of a cone:
- s = √(r² + h²)
- Lateral surface area of a cone:
- L = πrs = πr√(r² + h²)
- Base surface area of a cone:
- B = πr²
- Total surface area of a cone:
- A = L + B = πrs + πr² = πr(s + r) = πr(r + √(r² + h²))
Where,
r is the radius
h is the height
s is slant height of cone
Volume of Conical Frustum Formula
- Volume of a conical frustum:
- V = (1/3)πh (r₁² + r₂² + (r₁ * r₂))
- Slant height of a conical frustum:
- s = √((r₁ - r₂)² + h²)
- Lateral surface area of a conical frustum:
- S = π * (r₁ + r₂) * s = π * (r₁ + r₂) * √((r₁ - r₂)² + h²)
- Top surface area of a conical frustum (a circle):
- T = πr₁²
- Base surface area of a conical frustum (a circle):
- B = πr₂²
- Total surface area of a conical frustum:
- A = π * (r₁² + r₂² + (r₁ + r₂) * s) = π * [ r₁² + r₂² + (r₁ + r₂) * √((r₁ - r₂)² + h²) ]
Where,
r₁ is the radius of circle1
r₂ is the radius of circle2
h is height
s is slant height
Volume of circular cylinder formula
Circular cylinder is having two circles of equal radii one on the bottom one is at the top. Two straight and parallel lines joins those circles. Its formula is
- Calculate volume of a cylinder:
- V = πr²h
- Calculate the lateral surface area of a cylinder:
- L = 2πrh
- Calculate the top and bottom surface area of a cylinder:
- T = B = πr²
- Total surface area of a closed cylinder is:
- A = L + T + B = 2πrh + 2(πr²) = 2πr(h+r)
Where,
r is the circle radius
h is the height of cylinder