Tube Calculator
In geometry, a tube is a pipe-shaped object. It is a cylinder with a hollow space inside. Straw is the best example of a tube.
Tube Calculator: Want to calculate the unknown measures of a tube in a simple way? Then you must try out this easy to operate tool provided over here. It is one of the best and easiest ways that you can ever find the tube radius, circumference, volume, height, and others. This page is all about computing the measurements of a tube easily. Here you can check an interactive tutorial explaining each step of the process and formulas.
Avail free user-friendly Tube Calculator to get the volume, circumference, area, radius, and height of both circles within less time. Just enter the known parameters in the input fields shown below and hit on the calculate button to get the output as soon as possible.
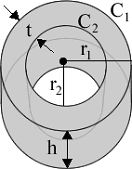
| outer radius r1 | r1 = |
| inner radius r2 | r2 = |
| outer circumference C1 | C1 = |
| inner circumference C2 | C2 = |
| height | h = |
| wall thickness | t = |
| outer surface area L1 | L1 = |
| inner surface area L2 | L2 = |
| end surface area | A = |
| volume within C1 | V1 = |
| volume within C2 | V2 = |
| volume of solid | V = |
Tube Formulas
Make use of these simple formulas to calculate the circumference, area, volume, thickness of the cube.
- Circumference of the Tube Formula:
- Outer Circumference C = 2πR
- Inner Circumference c = 2πr
- Lateral Surface Area of the Tube Formula:
- Outer Surface Area L = 2πRh
- Inner Surface Are l = 2πrh
- Area for the cross-section of the Tube Formula:
- The area enclosed by outer circumference A = πR²
- The area enclosed by the inner circumference a = πr²
- Area for the solid cross-section of the tube K = π(R² - r²)
- The volume of the Cylinder Formula:
- The volume enclosed by outer circumference V = πR²h
- The volume enclosed by the inner circumference v = πr²h
- The volume of the solid tube O = π(R² - r²)h
- The thickness of the tube Formula:
- Thickness t = R - r
Tube Calculations:
- If circumferences, and the height of the tube are given, then
- Outer radius R = C / 2π
- Inner radius r = c / 2π
- Wall thickness t = R - r
- Outer surface area L = Ch
- Inner surface area l = ch
- End surface area K = π(R² - r²)
- Volume within outer circumference V = C²h / 4π
- Volume within inner circimference v = c²h / 4π
- The volume of solid O = π(R² - r²)h
- If the outer radius, thickness, and height of a tube are given then
- The area enclosed by outer circumference A = πR²
- Outer circumference C = 2πR
- Inner radius r = R - t
- Inner circumference c = 2π(R - t)
- Area enclosed by the inner circumference a = π(R - t)²
- End Area K = π(t² - 2Rt)
- The volume enclosed by outer circumference V = πR²h
- The volume enclosed by the inner circumference v = π(R - t)h
- Volume of solid O = π(t² - 2Rt)h
- If the inner radius, thickness, and height of the tube are known, then
- Outer radius R = t + r
- Inner circumference c = 2πr
- Outer circumference C = 2π(t + r)
- Outer Surface Area L = 2π(t + r)h
- Inner Surface Are l = 2πrh
- Area enclosed by outer circumference A = π(t + r)²
- Area enclosed by the inner circumference a = πr²
- Area for the solid cross-section of the tube K = π(t² + 2tr)
- Volume enclosed by outer circumference V = π(t + r)²h
- Volume enclosed by the inner circumference v = πr²h
- Volume of the solid tube O = π((t² + 2tr)h
- If inner, outer radii, the volume of the tube are given, then
- Outer circumference C = 2πR
- Area enclosed by outer circumference A = πR²
- Inner circumference c = 2πr
- The area enclosed by the inner circumference a = πr²
- Area for the solid cross-section of the tube K = π(R² - r²)
- Height h = O / π(R² - r²)
- Volume enclosed by outer circumference V = πR² * [O / π(R² - r²)]
- Volume enclosed by the inner circumference v = πr² * [O / π(R² - r²)]
- Outer Surface Area L = 2πR * [O / π(R² - r²)]
- Inner Surface Are l = 2πr * [O / π(R² - r²)]
- Thickness t = R - r
- If the circumferences, volume of a tube are given, then
- Outer radius R = C / 2π
- Inner radius r = c / 2π
- Height h = O / π(R² - r²)
- Volume enclosed by outer circumference V = [C²/ 4π] * [O / π(R² - r²)]
- Volume enclosed by the inner circumference v = [c² / 4π] * [O / π(R² - r²)]
- Area enclosed by outer circumference A = C²/ 4π
- The area enclosed by the inner circumference a = c² / 4π
- Area for the solid cross-section of the tube K = (C² - c²) / 4π
- Thickness t = (C - c) / 2π
- Outer Surface Area L = C[O / π(R² - r²)]
- Inner Surface Are l = c[O / π(R² - r²)]
- If the outer radius, thickness, and volume of the tube are known, then
- Inner radius r = R - t
- Height h = O / π(t² - 2Rt)
- Outer circumference C = 2πR
- Inner Circumference c = 2π(R - t)
- Volume enclosed by outer circumference V = πR² * [O / π(t² - 2Rt)]
- Volume enclosed by the inner circumference v = π(R - t)² * [O / π(t² - 2Rt)]
- Outer Surface Area L = 2πR * [O / π(t² - 2Rt)]
- Inner Surface Are l = 2π(R - t) * [O / π(t² - 2Rt)]
- The area enclosed by outer circumference A = πR²
- The area enclosed by the inner circumference a = π(R - t)²
- Area for the solid cross-section of the tube K = π(t² - 2Rt)
- If the outer circumference, thickness, and volume of the tube are given, then
- Outer radius R = C / 2π
- Inner radius r = C / 2π - t
- Height h = O / [π((C / 2π)² - (C / 2π - t)²)]
- Inner circumference c = 2π * (C / 2π - t)
- Outer Surface Area L = C * [O / [π((C / 2π)² - (C / 2π - t)²)]]
- Inner Surface Are l = 2π * (C / 2π - t)h
- The area enclosed by outer circumference A = C² / 4π
- The area enclosed by the inner circumference a = C²π / (2π - t)²
- Area for the solid cross-section of the tube K = π((C / 2π)² - (C / 2π - t)²)
- The volume enclosed by outer circumference V = πR²h
- The volume enclosed by the inner circumference v = πr²h
Where, R is the outer radius
r is the inner radius
C is the outer circumference
c is the inner circumference
L is the outer surface area
l is the inner surface area
V is the volume within the outer circumference
v is the volume within the inner circumference
h is the height
t is the wall thickness
O is the volume of solid
K is the end surface area
A is the area enclosed by outer circumference
a is the area enclosed by the inner circumference
Steps to Find Tube Volume, Area
Follow the below-provided step by step process to get the unknown parameters of a tube easily.
Tube Circumference:
- Get the outer radius, inner radius from the question.
- Multiply the outer radius with double of π to check outer circumference.
- Multiply inner radius with 2π to find the inner circumference.
Tube Thickness:
- Find out the inner and outer radius of the tube.
- Subtract the outer radius from the inner radius to get the thickness.
Tube Volume:
- Check out the radii, height of the tube from the question.
- Square the radius and multiply it with π to know outer, inner volume.
- Subtract outer radius square from the inner radius square.
- Multiply subtracted value with π, height to get the solid volume.
Tube Inner Radius:
- Process 1:
- Obtain the inner circumference.
- Divide the inner circumference by 2π to see the inner radius value.
- Process 2:
- Get the wall thickness, outer radius.
- Subtract outer radius from the wall thickness to check the inner radius value.
Tube Outer Radius:
- Process 1:
- Note down the tube thickness, inner radius.
- Add thickness to the inner radius to get the outer radius.
- Process 2:
- Check the outer circumference of the tube.
- Divide the circumference by 2 times of π.
- The obtained value is called the outer radius.
Tube End Surface Area:
- Square outer, inner radii of the tube.
- Multiply the radius with π to find the outer, inner areas.
- Subtract the outer radius square from the inner radius square.
- Multiply the result with π to see the area for the solid cross-section of the tube.
Tube Lateral Surface Area:
- Observe the radii, height.
- Multiply 2π, height, and radii to check the inner, outer lateral surface areas.
Tube Height:
- Make a note of the tube volume.
- Square the radii.
- Subtract the outer radius square from the inner radius square.
- Multiply subtracted value with π.
- Divide the volume by the result to get tube height.
Solved Example Questions on Tube Calculator
Example 1: Find the tube outer circumference, inner radius, volume end surface area. If the tube outer radius is 20 mm, the inner circumference is 94.2 mm, height is 10 mm.
Solution:
Given that,
Outer radius R = 20 mm
Inner circumference c = 94.2 mm
Height h = 10 mm
inner radius formula is r = c / 2π
r = 94.2 / 2π
= 94.2 / (2 * 3.14) = 94.2 / 6.28
= 15 mm
Outer Circumference C = 2πR
C = 2π * 20
= 2 * 3.14 * 20 = 125.6 mm
Area enclosed by outer circumference A = πR²
A = π * 20² = 3.14 * 20 * 20
= 1,256 mm²
Area enclosed by the inner circumference a = πr²
a = π * 15² = 3.14 * 15 * 15
= 706.5 mm²
Area for the solid cross section of the tube K = π(R² - r²)
K = π * (20² - 15²)
= 3.14 * (400 - 225)
= 3.14 * 175 = 549.5 mm²
Outer Surface Area L = 2πRh
L = 2 * 3.14 * 20 * 10
= 1,256 mm²
Inner Surface Are l = ch
= 94.2 * 10
= 942 mm²
Thickness t = R - r
t = 20 - 15
= 5 mm
Volume enclosed by outer circumference V = πR²h
V = π * 20² * 10
= 10π * 20 * 20
= 10π * 400 = 4000π
= 4000 * 3.14
= 12,560 mm³
Volume enclosed by the inner circumference v = c²h / 4π
v = (94.2² * 10) / 4π
= (94.2 * 94.2 * 10) / (4 * 3.14)
= 88,736.4 / 12.56 = 7,065 mm³
Volume of the solid tube O = π(R² - (c/ 2π)²)h
O = π(20² - (94.2/ (2 * 3.14))²) * 10
= π(20 * 20 - (94.2/ 6.28)²) * 10
= π(400 - 15²) * 10
= π(400 - 225) * 10 = 175 * 10 * π
= 1750π = 1750 * 3.14
= 5,495 mm³
∴ Tube inner radius is 15 mm, outer radius is 20 mm, thickness is 5 mm, outer circumference is 125.6 mm, inner circumference is 64.2 mm, Outer lateral surface area is 1,256 mm², inner lateral surface area is 942 mm², Area enclosed by outer circumference is 1,256 mm², Area enclosed by inner circumference is 706.5 mm², Area for the solid cross section of the tube is 549.5 mm², volume enclosed by outer circumference is 12,560 mm³, volume enclosed by inner circumference is 7,065 mm³, and volume of the cube is 5,495 mm³.
Example 2: The tube volume is 1586 cm³, the outer circumference is 120 cm, the thickness is 9 cm. Calculate the tube radii, circumference, volume, and surface area?
Solution:
Given that,
Volume O = 1586 cm³
Outer circumference C = 120 cm
Thickness t = 9 cm
Outer radius R = C / 2π
R = 120 / 2π
= 120 / (2 * 3.14) = 120 / 6.28
= 19.1 cm
Inner radius r = C / 2π - t
r = 120 / 2π - 9
= 120 / 6.28 - 9
= 19.1 - 9 = 10.1 cm
Height h = O / π((C / 2π)² - (C / 2π - t)²)
h = 1586 / [π((120 / 6.28)² - (120 / 2π - 9))²)]
= 1586 / [π(19.10² - (120/ 6.28 - 9)²)]
= 1586 / [π(365.12 - (19.10 - 9)²)]
= 1586 / [π(365.12 - (10.1)²)]
= 1586 / [π(365.12 - 102.01)]
= 1586 / [π(262.8)]
= 1586 / (262.8 * 3.14) = 1586 / 825.19
= 1.92 cm
Inner circumference c = 2π * (C / 2π - t)
c = 2* 3.14 * (120 / 6.28 - 9))
= 6.28 * (19.10 - 9)
= 10.1 * 6.28 = 63.42 cm
Outer Surface Area L = C * [O / π((C / 2π)² - (C / 2π - t)²)]
L = 120 * (1586 / [π((120 / 6.28)² - (120 / 2π - 9))²)])
= 120 * (1586 / [π(19.10² - (120/ 6.28 - 9)²)])
= 120 * (1586 / [π(365.12 - (19.10 - 9)²)])
= 120 * (1586 / [π(365.12 - (10.1)²)])
= 120 * (1586 / [π(262.8))
= 120 * 1586 / 826.04 = 120 * 1.92
= 230.4 cm²
Inner Surface Area l = 2π * (C / 2π - t)h
l = 6.28 * (120 / 6.28 - 9)) * 1.92
= 6.28 * (19.1 - 9)) * 1.92
= 10.1 * 6.28 * 1.92
= 121.78 cm²
Area enclosed by outer circumference A = C² / 4π
A = 120² / 12.56
= 14400 / 12.56 = 1,146.49 cm²
Area enclosed by the inner circumference a = C²π / (2π - t)²
a = 3.14 * 10.1²
= 102.01 * 3.14 = 320.31 cm²
Area for the solid cross section of the tube K = π((C / 2π)² - (C / 2π - t)²)
K = π((120 / 6.28)² - (120 / 6.28 - 9)²)
= π((19.1)² - (19.1 - 9)²)
= π(365.12 - (10.1)²)
= π(365.12 - 102.01) = 263.11π
= 263.11 * 3.14 = 826.16 cm²
Volume enclosed by outer circumference V = πR²h
V = 3.14 * 19.1² * 1.92 = 2,199.36 cm³
Volume enclosed by the inner circumference v = πr²h
v = 3.14 * 10.1² * 1.92 = 614.99 cm³
∴ Tube volume is 614.99 cm³, height is 1.92 cm, inner radius is 10.1 cm, outer radius is 19.1 cm, outer circumference is 120 cm, inner circumference is 63.45 cm, thickness is 9 cm, outer surface area is 23.054 cm², inner surface area is 121.9 cm², end surface area is 825.53 cm², outer volume is 2201.5 cm³, inner volume is 615.51 cm³.
Want to master geometry then use our different calculators prevailing on Areavolumecalculator.com and gain more knowledge on all math concepts.
FAQs on Tube Calculator
1. What is the formula to find the volume of a tube?
The simple formula to calculate the tube volume is π(outer_radius² - inner_radius²) * height. Substitute the values in this formula to compute the volume.
2. How do you find the cross-sectional area of the tube?
First of all, find the area of the outer cylinder and inner cylinder using formula π * radius². Then, subtract the outer area from the inner area to get the tube cross-sectional area.
3. How is outer diameter and inner diameter calculated?
You can calculate the outer diameter in 2 ways. One is simply by measuring the length of a line that passes through the center and touches two points on the outer part of the tube. Another method is double the outer, inner radius to get outer diameter and inner diameter. Subtract the outer diameter from the inner diameter to check the thickness.
