Triangle Calculator: Right
Right Angled Triangle is a polygon having three sides of different lengths and one of the angles is 90°. It is a closed polygon with three sides and vertices. Handy and quick online calculator that computes the right triangles perimeter, area, semiperimeters, sides length, angles, altitudes are available here.
You can easily calculate the unknown parameters of a right triangle by providing the known details in our Right Triangle Calculator. Select the known details and provide input details. Press on the calculate button to get the triangle area, perimeter, and other details.
| a = | |
| b = | |
| c = | |
| P = | |
| s = | |
| K = | |
| ha = | |
| hb = | |
| hc = |
The Formulas of A Right Triangle
A right triangle is a special case of the triangle where one angle is equal to 90 degrees. It is also called a right-angled triangle. In this triangle, the sum of squares of sides is equal to the square of hypotenuse known as the Pythagorean Theorem. The hypotenuse is the side that is opposite to the right angle vertex. Other formulas of the right triangle are mentioned here.
- Right angle triangle angle C = 90 degrees
- The Perimeter of a Right Triangle Formula:
- Perimeter P = a + b + c
- Area of a Right Triangle Formula:
- Area K = (a * b) / 2
- Semiperimreter of a Right Trinagle Formula:
- Semiperimeter s = (a + b + c) / 2
- Altitudes of a Right Triangle Formula:
- Altitude a of a triangle: ha = b
- Altitude b of a triangle: hb = a
- Altitude c of a triangle hc = (a * b) / c
- Pythagorean Theorem:
- In a right-angled triangle, the square of the hypotenuse is equal to the sum of squares of the other two sides.
- Pythagorean Theorem for Right Triangle: c² = a² + b²
- Right Triangle Angles Formulas:
- If β is given, α = 90 - β
- If α is given, β = 90 - α
- To Find α
- sin(α) = a / c, α = arcsin(a / c)
- cos(α) = b / c, α = arccos(b / c)
- tan(α) = a / b, α = arctan(a / b)
- cot(α) = b / a, α = arccot(b / a)
- To Find β
- sin(β) = b / c, β = arcsin(b / c)
- cos(β) = a / c, β = arccos(a / c)
- tan(β) = b / a, β = arctan(b / a)
- cot(β) = a / b, β = arccot(a / b)
Right Triangle Calculations:
This section includes the simple formulas to find the right triangle measurement when you know two sides or angle & one side or area and one side.
- If any two sides of a right triangle are known, then
- Using Pythagorean Theorem c = √(a² + b²) or b = √(c² - a²)
- Perimeter P = a + b + c
- Semiperimeter s = (a + b + c) / 2
- Area K = (a * b) / 2
- Altitude ha = b
- Altitude hb = a
- Altitude hc = (a * b) / c
- Angle α = arcsin(a / c)
- Angle β = arccos(a / c)
- If one side and angle of the right triangle are given, then
- β = 90 - α
- b = c * cos(α)
- Using pythagorean theorem a = √(c² - b²)
- Area K = (a * b) / 2
- Perimeter P = a + b + c
- Semiperimeter s = (a + b + c) / 2
- Altiude ha = b
- Altitude hb = a
- Altitude hc = (a * b) / c
- If area, one side of the triangle are given, then
- Side length b = 2K / a
- Side length c = √(a² + b²)
- Perimeter P = a + b + c
- Semiperimeter s = (a + b + c) / 2
- Angle α = arccos(b / c)
- Angle β = arcsin(b / c)
- Altitude ha = b
- Altitude hb = a
- Altitude hc = (a * b) / c
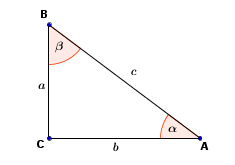
Where,
a, b , c are the sides of a right triangle.
A, B, C are the vertices
P is theright triangle perimeter
K is the area
s is the triangle semiperimeter
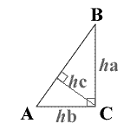
ha is the altitude drawn from vertex A
hb is the altitude drawn from vertex B
hc is the altitude drawn from vertex C
α, β are two angles of a triangle
How to calculate Right Triangle Area, Angles, Perimeter?
Finding the right triangle semiperimeter, area, perimeter, area, sides length, and altitudes means calculating the unknown measures of a triangle using the known parameters. The simplest ways to calculate the right triangle measurements are given below. Go through these useful steps and follow them.
Right Triangle Perimeter:
- Get three sides of the triangle.
- Sum up the sides to check the perimeter.
Right Triangle Area:
- Get any two sides of a triangle.
- Multiply the length of the sides.
- Divide the product by 2 to get the triangle area.
Right Triangle Semiperimeter:
- Find the length of the triangle sides.
- Add all the sides and divide it by 2 to check the semiperimeter.
Right Triangle Altitudes:
- Altitude is a line drawn from the vertex to the opposite side midpoint. or every triangle, we have three altitudes.
- Check the right angle three sides.
- Altitude a of the triangle is b.
- Altitude b of the triangle is a.
- Altitude c is obtained by calculating the product of a, b, and divide the obtained value by c.
Right Triangle Side Length:
- Process 1:
- Find the two sides' length of the triangle from the question.
- According to the Pythagorean theorem square the length of the given side.
- Add the squared values and apply the square root function to the result to get other side lengths.
- Process 2:
- Check side length, area of the triangle.
- Double the area, divide it by the given side length.
- Obtained is called second side length.
- The third side length can be calculated by substituting the values in the Pythagorean theorem formula.
- Do further required calculations.
- Process 3:
- Get one side length ad one angle.
- Multiply the given side with cos of angle to get the second side.
- Use the Pythagorean theorem to compute the third side length.
Right Triangle Angles:
- Find triangle sides from the question.
- Divide the first side by the third side.
- Find the arcsin of the result to get the first angle.
- Find the arccos of step 2 to get another angle.
Solved Examples
Example 1: If the right triangle area is 180 cm² and one side length is 12 cm. Calculate triangle other sides, angles, perimeter, semiperimeter, and altitudes?
Solution:
Given that,
Side length a = 12 cm
Area K = 180 cm²
Side length b = 2K / a
= (2 * 180) / 12
= 360 / 12 = 30 cm
Side length c = √(a² + b²) = √(12² + 30²)
= √(144 + 900)
= √(1044) = 32.31 cm
Perimeter P = a + b + c
= 32.31 + 12 + 30
= 74.31 cm
Semiperimeter s = (a + b + c) / 2
= (32.31 + 12 + 30) / 2
= (74.31) / 2
= 37.15 cm
Angle α = arctan(a / b)
= arctan(12 / 30)
= arctan(0.4)
= 21.8°
Angle β = arcsin(b / c)
= arcsin(30 / 32.31) = arcsin(0.928)
= 68.2°
Altitude ha = b
= 30 cm
Altitude hb = a
= 12 cm
Altitude hc = (a * b) / c
= (12 * 30) / 32.31
= 360 / 32.31 = 11.14 cm
∴ Right trinagle sides are 12 cm, 30 cm, 32.31 cm, area is 180 cm², perimeter is 74.31 cm, semiperimeter is 37.15 cm, altitudes are 12 cm, 30 cm, 11.14 cm, and angles are 21.8°, 68.2°.
Example 2: Right triangles sides are a = 10 m, b = 8 m, c = 12.806 m. What is the triangle area, perimeter, semiperimeter, altitudes, and angles?
Solution:
Given that,
Triangle sides a = 10 m, b = 8 m, c = 12.806 m
Right Triangle Perimeter P = a + b + c
= (10 + 8 + 12.806)
= 30.806 m
Semiperimeter s = (a + b + c) / 2
= (10 + 8 + 12.806) / 2
= 30.806 / 2 = 15.403 m
Area K = (a * b) / 2
= (10 * 8) / 2
= 80 / 2 = 40 m²
Altitude ha = b
= 8 m
Altitude hb = a
= 10 m
Altitude hc = (a * b) / c
= (10 * 8) / 12.806
= 80 / 12.806 = 6.247 m
Angle α = arcsin(a / c)
= arcsin(10 / 12.806) = 51.34°
β = 90 - α
= 90 - 51.34
= 38.66°
∴ Right triangle sides are 10 m, 8 m, 5 m, the area is 40 m², the perimeter is 23 m, semiperimeter is 11.5 m, altitudes are 8 m, 10 m, 16 m, and angles are 11.31°, 78.69°.
Check out free calculators at Areavolumecalculator.com to find any geometric shape area, volume, perimeter, etc easily.
FAQs on Right Triangle Calculator
1. How do you find the side length of a right-angled triangle?
You can use the Pythagorean theorem to find the side length of a right triangle. That states that the square of the hypotenuse is equal to the sum of squares of the other two sides.
2. How to find the angle of a right triangle?
The sum of three angles of a triangle is 180 degrees. We already know that one angle of the right triangle is 90°. Find the second angle by solving arccos(b / c). The third angle is obtained by subtracting 90° from the second angle.
3. How do you know if three points make a right triangle?
Simply substitute those sides in the Pythagorean theorem and check that. If that theorem satisfies, then those points form a right triangle.
4. What is meant by the Pythagorean Theorem?
Pythagorean Theorem explains the relation between the sides of a right-angled triangle. It states that in a right triangle, the square of the hypotenuse side is always equal to the sum of squares of other sides. Its formula is Hypotenuse² = Perpendicular² + Base² i.e c² = a² + b².
