Rhombus Calculator
The rhombus is a flat-shaped and four-sided quadrilateral. All the sides of a rhombus are in equal length, and opposite sides are parallel. The opposite angles of a rhombus are equal. The rhombus is also called a diamond. In the rhombus, the diagonals bisect each other at the right angles, and they meet at the center point of the rhombus.
Rhombus Calculator: Are you looking for a handy free calculator tool that provides the area, corner angles, perimeter, height, diagonals length, and the side length of a rhombus? If yes, then you have arrived at the correct place. This page gives complete information about the rhombus. Unlike other calculators, our rhombus calculator gives a detailed explanation involved in solving the question. You can also find the formulas and calculations that are useful to calculate the unknown parameters of a rhombus.
Enter side length, one corner angle in the input sections of the calculator, and press on the calculate button. You can check the area, perimeter, corner angles, and diagonals of a rhombus in a fraction of seconds.
| corner angles | A = C = |
| corner angles | B = D = |
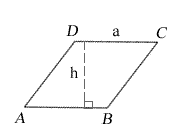
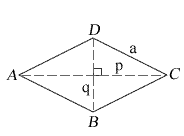
| side a length | a = |
| diagonal length | p = |
| diagonal length | q = |
| height | h = |
| perimeter | P = |
| area | K = |
Formulas of a Rhombus
Below given are the simple formulas that are useful to compute the area, perimeter, diagonals, and corner angles of a rhombus. Go through these formulas and solve the questions on rhombus easily.
- The Perimeter of a Rhombus Formula
- If the length of the side of a rhombus is given, then
- Perimeter P = 4s
- If the length of the side of a rhombus is given, then
- Area of a Rhombus Formulas
- If the side length, and the height of the rhombus are given, then
- Area K = sh
- If the side length and one angle is given, then
- Area K = s² sin(A)
- If the diagonals of a rhombus are given, then
- Area K = (p * q) / 2
- If the side length, and the height of the rhombus are given, then
- Diagonlas of a Rhombus Formulas:
- If the side length and corner angle are given, then
- Diagonal 1 is p = s √( 2 + 2 cos(A) ) = s √( 2 - 2 cos(B) )
- Diagonal 2 is q = s √( 2 - 2 cos(A) ) = s √( 2 + 2 cos(B) )
- p² + q² = 4s²
- If the side length and corner angle are given, then
- Height of a Rhombus Formula:
- If side length and one corner angle is given, then
- Height h = s sin(A)
- If side length and one corner angle is given, then
- Corner Angles of a Rhombus Formulas:
- If one corner angle A is given, then
- B = 180° - A
- C = A
- D = B
- A + B = 180° = π radians
- for a rhombus that is not a square,
- 0 < A< 90° (0 < A < π/2)
- 90° < B < 180° (π/2 < B < π)
- Side Length of a Rhombus Formulas:
- If perimeter of a rhombus is given, then
- Side length s = P / 4
- If area, height of a rhombus are given, then
- Side length s = K / h
- If height, angle of a rhombus are given, then
- Side length s = h / sin(A)
- If perimeter of a rhombus is given, then
Rhombus Calculations:
These rhombus calculations are helpful to find the unknown parameters of a rhombus using the given details.
- If diagonals of a rhombus are given, then
- Side length of the rhombus s = √(p² + q²) / 2
- The perimeter of a rhombus P = 4s
- Area of the rhombus K = (p * q) / 2
- Corner angle A = arcsin( K / s²)
- B = 180° - A
- C = A
- D = B
- Height h = s sin(A)
- If area, one diagonal of a rhombus are given, then
- Second diagonal length q = 2K / p
- Side length of a rhombus s = √(p² + q²) / 2
- Corner angle A = arccos( 1 + (q² / 2s²) )
- Height of a rhombus h = s sin(A)
- The rhombus perimeter P = 4s
- B = 180° - A
- C = A
- D = B
- If the corner angle and height of a rhombus are given, then
- Side length of a rhombus s = h / sin(A)
- Rhombus perimeter P = 4s
- First diagonal of a rhombus p = √( 2s² + 2s² cos(A) )
- Second diagonal of a rhombus q = √( 2s² - 2s² cos(A) )
- Area of a rhombus K = s² sin(A)
- B = 180° - A
- C = A
- D = B
- If the area, height of a rhombus are given, then
- The side length of a rhombus s = K / h
- Rhombus perimeter P = 4s
- First diagonal length of a rhombus p = √( 2s² + 2s² cos(A) )
- Second diagonal length of a rhombus q = √( 2s² - 2s² cos(A) )
- Corner angle A = arcsin(K/s²)
- B = 180° - A
- C = A
- D = B
- If side length, area of a rhombus are given, then
- Corner angle A = arcsin(K/s²)
- One diagonal is p = √( 2s² + 2s² cos(A) )
- Other diagonal is q = √( 2s² - 2s² cos(A) )
- Height of a rhombus h = s sin(A)
- Rhombus perimeter P = 4s
- B = 180° - A
- C = A
- D = B
- If side length, the height of a rhombus are given, then
- Perimeter P = 4s
- Corner angle A = arcsin(h/s)
- Diagonal 1 is p = √( 2s² + 2s² cos(A) )
- Second diagonal is q = √( 2s² - 2s² cos(A) )
- Area is K = s² sin(A)
- B = 180° - A
- C = A
- D = B
- If side length and diagonal of a rhombus are given, then
- Corner angle A = arccos( 1 + (q² / 2s²) )
- Other diagonal length p = √( 2s² + 2s² cos(A) )
- Height of a rhombus h = s sin(A)
- Perimeter P = 4s
- Area K = s² sin(A)
- B = 180° - A
- C = A
- D = B
- If side length, corner angle of a rhombus are given, then
- Diagonal 1 length of a rhombus is p = √( 2s² + 2s² cos(A) )
- Diagonal 2 length of a rhombus q = √( 2s² - 2s² cos(A) )
- Rhombus perimeter P = 4s
- Height of a rhombus h = s sin(A)
- Rhombus area K = s * h
- B = 180° - A
- C = A
- D = B
Where,
h is the rhombus height
A, B, C, D are the corner angles of a rhombus
P is the rhombus perimeter
p is the shorter diagonal of a rhombus
q is the longer diagonal of a rhombus
s is the side length of a rhombus
K is the rhombus area
A, B and C, D are the adjacent angles
A, C and B, D are the opposite angles
How to Calculate the Rhombus Area, Perimeter, Diagonals?
Rhombus is a quadrilateral having 4 corners and 4 sides of equal length. The opposite angles of a rhombus are equal and the sum of angles is equal to 360°. The diagonals bisect each other at right angles. Here we are giving the step by step procedure to solve the rhombus perimeter, area, diagonals, and corner angles. Follow these steps carefully
Rhombus Area:
- Process 1:
- Get the length of diagonals of a rhombus from the question.
- Find the product of diagonals and get half of it.
- The obtained value is the rhombus area.
- Process 2:
- Observe side length, one corner angle of the rhombus.
- Square the side length.
- Get the sine function of the angle in degrees.
- Multiply step 2 and 3 to get the area.
- Process 3:
- Make a note of the side length and height of the rhombus.
- Multiply those two to check the rhombus area.
Rhombus Perimeter:
- Get the length of the side of a rhombus from the question.
- Multiply the side by four times to get its perimeter.
Rhombus Height:
- Get the side length and corner angle of a rhombus.
- Find the sine function of the corner angle.
- Multiply it with the side to check the height of a rhombus.
Rhombus Diagonals:
- Process 1:
- Check side length and one angle of the rhombus.
- Find the cosine function of the corner angle.
- Double the result and add, subtract 2 to it.
- Apply the square root function and multiply it with the side length to get both diagonals lengths.
- Process 2:
- Get the cosine of the corner angle.
- Square the side length and multiply it by 2.
- Multiply step 2 with step 1.
- Add step 2 and step 4 and apply the square root to get one diagonal length.
- Subtract step 4 from step 2 and apply the square root to get the other diagonal length.
Side Length of a Rhombus:
- Process 1:
- Get rhombus area, height from the question.
- Divide the area by height to get side length.
- Process 2:
- Make a note of the corner angle, the height of the rhombus.
- Find the sine function of the corner angle.
- And divide the height by the obtained value to get side length.
- Process 3:
- Check the rhombus perimeter from the question.
- Divide it by 4 to find the rhombus area.
Corner Angles of a Rhombus:
- Process 1:
- Get the one corner angle from the question.
- Subtract 180° from the given angle to get the adjacent angle value.
- Equate the opposite angles.
- Process 2:
- Note down the area, side length from the question.
- Divide the area by square of side length.
- Get the arcsin of obtained value to get one corner angle.
- Follow the process one to get other angles of a rhombus.
- Process 3:
- Make a note of the diagonal length, the side length of the rhombus.
- Divide the square of diagonal by double square of side length.
- Add one to the obtained value.
- Find the arccos of the value got from the above step to find one corner angle.
- Follow process 1 to check other corner angles.
Example Questions
Example 1: Find the height, perimeter, diagonals length, and corner angle of a rhombus? If the rhombus area is 190 m² and its side length is 28 m.
Solution:
Given that,
Area K = 190 m²
Side length s = 28 m
Corner angle A = arcsin (K / s²)
= arcsin (190 / 28²)
= arcsin (190/784)
= arcsin (0.242)
= 14.025°
B = 180° - A
= 180° - 14.025°
= 165.97°
C = 14.025°
D = 165.97°
One digaonal length p = √( 2s² + 2s² cos(A) )
= √( 2(28)² + 2(28)² cos(14.025) )
= √( 2(784) + 2(784) cos(14.025) )
= √( 1568 + 1568 cos(14.025) )
= √( 1568 + 1568 * 0.111)
= √( 1568 + 174.04)
= √(1742.048)
= 41.737
Second diagonal length q = √( 2s² - 2s² cos(A) )
= √( 2(28)² - 2(28)² cos(14.025) )
= √( 2(784) - 2(784) cos(14.025) )
= √( 1568 - 1568 cos(14.025) )
= √( 1568 - 1568 * 0.111)
= √( 1568 - 174.04)
= √1,393.96
= 37.33
Perimeter P = 4s
= 4 * 28
= 112
Height h = s sin(A)
= 28 * sin(14.025)
= 28 * 0.993
= 27.804
∴ Rhombus height is 27.804 m, the perimeter is 112 m, diagonals length is 55.581 m, 6.836 m, Corner angles are 14.025°, 165.974°, and the area is 190 m².
Example 2: If shorter and longer diagonals of a rhombus are 15 feet, 25 feet, calculate rhombus area, perimeter, height, side length, and corner angles?
Solution:
Given that,
Shorter diagonal length p = 15 feet
Longer diagonal length q = 25 feet
Side length of the rhombus s = √(p² + q²) / 2
= √(15² + 25²) / 2
= √(225 + 625) / 2
= √(850) / 2
= 29.15 / 2
= 14.57
The perimeter of a rhombus P = 4s
= 4 * 14.57
= 58.309
Area of the rhombus K = (p * q) / 2
= (15 * 25) / 2
= 375 / 2
= 187.5
Corner angle A = arcsin( K / s²)
= arcsin( 187.5 / 14.57²)
= arcsin( 187.5 / 212.284)
= arcsin( 0.8832)
= 61.927
B = 180° - A
= 180° - 61.927
= 118.07
C = A = 61.927
D = B = 118.07
Height h = s sin(A)
= 14.57 * sin(61.927)
= 14.57 * 0.7863
= 11.45
∴ Rhombus height is 11.45 feet, the perimeter is 58.309 feet, diagonals lengths are 15 feet, 25 feet, Corner angles are 61.927°, 118.07°, and the area is 187.5 feet².
Want to explore more maths concepts & make all your calculations much easier and faster then go with our website Areavolumecalculator.com and click on the available different geometry calculators links to access.
FAQs on Rhombus Calculator
1. Mention the properties of a rhombus?
All the sides of a rhombus are equal. The opposite sides are parallel. Opposite angles are equal. The diagonals bisect each other at right angles. The sum of adjacent interior angles is 180 degrees.
2. Are all sides of a rhombus equal?
Yes, all the sides of a rhombus are in equal length. It is one of the important properties of the rhombus.
3. What is the difference between rhombus and square?
The diagonals of a square have the same length while rhombus diagonals are of different lengths. All the interior angles of a square are 90 degrees, and the opposite angles of a rhombus are the same.
4. What is an example of a rhombus?
Rhombus can be found in different things around us. The best examples of a rhombus are kite, windows of a car, rhombus-shaped earrings, section of a baseball field, mirror, etc.
