Rectangle Calculator
Rectangle Calculator is a free online tool that supports you to calculate the perimeter, area, diagonal length and sides length of a rectangle easily. Provide any two values in the input section and calculate the unknown things by hitting on the calculate button. Our handy calculator not only gives the exact result but also provides the step by step procedure to find the rectangle parameters.
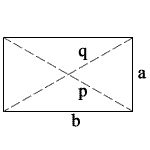
| side length | a = |
| side length | b = |
| diagonal | p = q = |
| perimeter | P = |
| area | A = |
Formulas of a Rectangle
The rectangle is a quadrilateral having four sides and four right angles. Opposite sides of a rectangle are in equal length. And opposite sides of a rectangle are parallel to each other. Here we are giving the simple formulas to calculate the rectangle perimeter, area, side length, and diagonal. Make use of these formulas and solve the questions effectively.
- Area of a Rectangle Formula:
- A = a * b
- Rectangle Perimeter Formula:
- P = 2a + 2b = 2(a + b)
- Diagonals of a Rectangle Formula:
- p = q = √(a² + b²)
Rectangle Calculations:
These rectangle calculations are helpful to solve the unknown parameters with the given information.
- If sides of a rectangle are given, then
- Rectangle Area A = ab
- Perimeter P = 2(a + b)
- Diagonals length p = q = √(a² + b²)
- If Area, one side length of a rectangle are given, then
- Other side length b = A / a
- Perimeter P = 2(a + b)
- Diagonals length p = q = √(a² + b²)
- If the perimeter and side length of a rectangle is given, then
- Other side length of a rectangle is b = (P - 2a) / 2
- Rectangle area A = ab
- Diagonals length of a rectangle p = q = √(a² + b²)
- If diagonals length, side of a rectangle are given, then
- Another side length of a rectangle is b = √(p² - a²)
- Area of rectangle is A = ab
- Perimeter of a rectangle P = 2(a + b)
Where,
P is the perimeter of a rectangle
p, q are the length of diagonals of a rectangle
a, b are the length of sides of a rectangle
A is the rectangle area
How to find Area, Perimeter, Diagonals of Rectangle?
Get the step by step procedure to compute the area, diagonals, perimeter, and side length of a rectangle from the below sections. Follow these instructions and guidelines while solving the questions.
Area of a Rectangle:
- Observe the length, breadth of a rectangle from the question.
- Multiply the rectangle's length and breadth to get the area.
Rectangle Perimeter:
- Get the length, breadth, or sides of a rectangle from the question.
- Add up the length, breadth of the rectangle.
- Double the obtained value to get a rectangle perimeter.
Diagonals of a Rectangle:
- Square both sides of a rectangle.
- Sum up the values and apply the square root function to it.
- The obtained value is the diagonal of a rectangle.
Length of Side of a Rectangle:
- Process 1:
- Check area, length, or breadth of a rectangle.
- Divide area by the given side to get the other side length.
- Process 2:
- Get one side length, the perimeter of a rectangle.
- Multiply the given side length by 2 and subtract it from the perimeter.
- Divide the obtained value by 2 to find the other side length.
- Process 3:
- Note down diagonal, one side of a rectangle.
- Square the diagonal, side length.
- subtract squared side length from the squared diagonal.
- Apply square root to the obtained value to find other side lengths of the rectangle.
Example Questions of Rectangle
Example 1: A rectangle is having a length of 5 cm, breadth of 8 cm. Find out the perimeter, diagonals length, area of a rectangle?
Solution:
Given that,
Length of rectangle a = 5 cm
Breath of rectangle b = 8 cm
Perimeter of a rectangle formula is P = 2a + 2b
= 2 * 5 + 2 * 8
= 10 + 16
= 26
Rectangle area is A = a * b
= 5 * 8
= 40
Diagonals length of a rectangle p = q = √(a² + b²)
= √(5² + 8²)
= √(25 + 64)
= √89
= 9.43
∴ Area of rectangle is 40 cm², perimeter is 26 cm, and diagonals are 9.43 cm.
Example 2: If the diagonal of a rectangle is 12 m, side length is 20 m, then what is the other side length, perimeter, and area of the rectangle?
Solution:
Given that,
Diagonal of a rectangle p = 12 m
Side of length of a rectangle b = 20 m
Other side length is a = √(p² - b²)
Substitue the values in the above formula
a = √(12² - 20²)
= √(144 - 400)
= √(256)
= 16
Area of rectangle A = ab
= 16 * 20
= 320
Rectangle perimeter P = 2(a + b)
= 2(16 + 20)
= 2(36)
= 72
∴ Perimeter of rectangle is 72 m, area is 320 m², sides of rectangle are 20 m, 16 m.
FAQs on Rectangle Calculator
1. What is the relationship between the area, perimeter, and diagonal of a rectangle?
The relationship between the perimeter, area, and diagonals of a rectangle is given here:
perimeter / 2 = diagonals² + 2 area
P / 2 = p² + 2A
2. What are the properties of a rectangle?
The five properties of a rectangle are:
It is a quadrilateral.
The opposite sides are parallel and equal in length.
Each interior angle is equal to 90° and the sum of the interior angles is 360°.
Both diagonals bisect each other.
Diagonals have the same length.
3. How do you calculate the diagonal of a rectangle?
The square of diagonal is equal to the sum of the square of the sides of a rectangle.
diagonal² = length of rectangle² + breadth of rectangle²
p² = a² + b²
4. Which website offers the best calculator to find the area, diagonal, the perimeter of a rectangle?
Areavolumecalculator.com is an ultimate website that offers best calculator to get the rectangle area, perimeter, and diagonals length.
