Square Pyramid Calculator
A square pyramid is a three-dimensional geometric shape having a square as the base and four triangular faces that meet at a single point called the apex. If all the triangular faces are in equal length, then it is called an equilateral square pyramid.
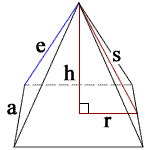
| height | h = |
| slant height | s = |
| slant length | a = |
| lateral edge length | e = |
| 1/2 side length | r = |
| volume | V = |
| lateral surface area | L = |
| base surface area | B = |
| total surface area | A = |
The Formulas of Square Pyramid
The geometrical formulas to calculate the square pyramid lateral edge length, slant height, radius, volume, lateral surface area, base surface area, and total surface area are mentioned below. Have a look at that and use it for solving various questions.
- Volume of the Square Pyramid Formula:
- Volume V = (1/3)a²h
- Lateral Surface Area of a Square Pyramid Formula:
- Lateral Surface Area L = a√(a² + 4h²)
- Base Surface Area of a Square Pyramid Formula:
- Base Surface Area B = a²
- Total Surface Area of a Square Pyramid Formula:
- Total Surface Area A = L + B = a² + a√(a² + 4h²)) = a(a + √(a² + 4h²))
- Slant Height of the Square Pyramid Formula:
- Slant Heigh s = √(h² + (1/4)a²)
- The radius of a Square Pyramid Formula:
- Radius r = a / 2
- Lateral Edge Length of Square Pyramid Formula:
- Lateral Edge Length e = √(h² + (1/2)a²)
Square Pyramid Calculations:
These formulas are useful to find the unknown parameters such as pyramid radius, slant height, height, total surface area, base surface area, lateral surface area, and lateral edge length easily.
- If volume, side length of the square pyramid are given, then
- Height h = 3V / a²
- Slant height s = √(9V²/aΓü┤ + (1/4)a²)
- Lateral edge Length e = √(9V²/aΓü┤ + (1/2)a²)
- Radius r = a / 2
- Lateral Surface Area L = a√(a² + 36V²/aΓü┤)
- Base surface area B = a²
- Total surface area A = a√(a² + 36V²/aΓü┤) + a²
- If the square pyramid total surface area, side length are known, then
- Height h = (1/2)√[(A - a² / a)² - a²]
- Base surface area B = a²
- Lateral Surface Area L = a√(a² + 4h²)
- Slant Height s = √(h² + (1/4)a²)
- Lateral Edge Length e = √(h² + (1/2)a²)
- Radius r = a / 2
- Volume V = (1/6)a²√[(A - a² / a)² - a²]
- If the pyramid slant height and side length are given, then
- Height h = √[s² - (1/4)a²]
- Volume V = (1/3)a²√[s² - (1/4)a²]
- Lateral Edge Length e = √(s² + (1/4)a²)
- Base surface area B = a²
- Lateral Surface Area L = 2as
- Total Surface Area A = a² + 2as
- If side length, lateral edge length are given, then
- Height h = √(e² - (1/2)a²)
- Lateral Surface Area L = a√(4e² - a²)
- Base surface area B = a²
- Total Surfcae Area A = a√(4e² - a²) + a²
- Slant height s = √(e² - (1/4)a²)
- Volume V = (1/3)a²√(e² - (1/2)a²)
- If the height, volume of the pyramid are known, then
- Side length a = √(3V / h)
- Slant Height s = √(h² + (3V/4h))
- Lateral edge length e = √(h² + (3V/2h))
- Base surface area B = 3V / h
- Lateral Surface Area L = a√(a² + 4h²)
- Total surface Area A = 3V / h + a√(a² + 4h²)
- If height, slant height of the square pyramid are given, then
- Side length a = 2√(s² - h²)
- Lateral Surface Area L = 4s√(s² - h²)
- Lateral edge length e = √(2s² - h²)
- Base surface area B = 4(s² - h²)
- Total surface area A = 4s√(s² - h²) + 4(s² - h²)
- Volume V = (4h/3) * (s² - h²)
- If height, lateral edge length of the square pyramid are known, then
- Side length a = √2(e² - h²)
- Slant height s = √(1/2) (e² - h²)
- Volume V = (2h/3)(e² - h²)
- Lateral surface area L = a√(a² + 4h²)
- Base surface area B = 2(e² - h²)
- Total surface area A = a√(a² + 4h²) + 2(e² - h²)
- If the side length, height of the square pyramid are known, then
- Lateral Edge Length e = √(h² + (1/2)a²)
- Slant Heigh s = √(h² + (1/4)a²)
- Lateral Surface Area L = a√(a² + 4h²)
- Base Surface Area B = a²
- Total Surface Area A = L + B = a² + a√(a² + 4h²)) = a(a + √(a² + 4h²))
- Volume V = (1/3)a²h
- Radius r = a / 2
- If the square pyramid base surface area, height are given, then
- Side Length a = √B
- Volume V = (1/3)Bh
- Lateral Edge Length e = √(h² + (1/2)B)
- Slant Heigh s = √(h² + (1/4)B)
- Lateral Surface Area L = √B * √(B + 4h²)
- Total Surface Area A = L + B = B + √B * √(B + 4h²)) = √B * (√B + √(B + 4h²))
- Radius r = √B / 2
Where,
a is the square side length
s is the slant height of the pyramid
e is the lateral edge length of the square pyramid
h is the pyramid height
L is the lateral surface area
B is the base surface area
A is the total surface area
V is volume
r is radius
Process to calculate Square Surface Volume, Area, Slant Height
Check out the below-listed detailed step by step process on finding the unknown measures of a square pyramid in a simple and easy manner. They are along the lines
Square Pyramid Slant Height:
- Observe the height, a side length of the square pyramid.
- Square the height.
- Divide side length square by 4.
- Add those values and apply square root to get the slant height.
Square Pyramid Volume:
- Check out the square pyramid side length, height.
- Multiply the height, side length square.
- Divide the result by 3 to find the volume.
Square Pyramid Lateral Surface Area:
- Note down the height, side length.
- Add 4 times of height square, side length square.
- Apply square root to the obtained value and multiply it with side length.
Square Pyramid Radius:
- Get the square pyramid side length.
- Divide it by 2 to check the radius.
Square Pyramid Base Surface Area:
- Make a note of the square side length.
- The Square of side length is the base surface area.
Square Pyramid Height:
- Process 1:
- Check total surface area, side length of the pyramid from the given question.
- Subtract the side length square from the total surface area.
- Divide the obtained value by side length.
- Subtract side length square from the square of the radius.
- Apply square root and divide it by 2 to get the height.
- Process 2:
- Obtain volume, side length.
- Divide 3 times of volume by side length square to check the height.
- Process 3:
- Find slant height, the side length of the pyramid.
- Divide the side length square by 4.
- Subtract slant height square from the result, and apply Square root to the obtained value.
- Process 4:
- Divide the side length square by 2.
- Subtract it from the square of lateral edge length.
- Apply square root to the result to know height.
Square Pyramid Lateral Edge Length:
- Find side length, height of the pyramid.
- Divide the side length square by 2.
- Add it to the height square.
- Calculate the square root of result to get lateral edge length.
Square Pyramid Total Surface Area:
- Perform the sum of lateral surface area, base surface area to see the total surface area of the square pyramid.
Square Pyramid Side Length:
- Process 1:
- Get base surface area.
- Square root of the base surface area is the side length.
- Process 2:
- Check slant height, height of the pyramid.
- Subtract height square from the slant height square.
- Apply square root to the result and multiply it with 2.
- Process 3:
- Obtain volume, pyramid height.
- Divide 3 times of volume by height.
- Apply square root to it to find square pyramid side length.
- Process 4:
- Note down lateral edge length, height.
- Subtract height square from the lateral edge length square.
- Double the result and apply square root to it to check the side length.
Examples Questions of Square Pyramid
Example 1: Find the square pyramid side length, radius, slant height, lateral surface area, base surface area, total surface area, and volume? If the pyramid lateral edge length is 35 m, height is 29 m.
Solution:
Given that,
Square Pyramid lateral edge length e = 35 m
Height of the pyramid h = 29 m
Side length a = √[2(e² - h²)]
a = √[2(35² - 29²)]
a = √[2(1225 - 841)] = √(2 * 384)
a =√768 = 27.71 m
Slant height s = √[(1/2) (e² - h²)]
s = √[(1/2) (35² - 29²)]
s = √[(1/2) (1225 - 841)]
= √[(1/2) (384)]
= √192 = 13.85 m
Volume V = (2h/3)(e² - h²)
V = ((2 * 29/3)(35² - 29²)
= (58/3)(1225 - 841)
= 19.33 * 384 = 7,424 m³
Lateral surface area L = a√(a² + 4h²)
L = 27.71√(27.71² + 4 * 29²)
= 27.71√(767.84 + 4 * 841)
= 27.71√(767.84 + 3,364)
= 27.71 * √4,131.84
= 27.71 * 64.27 = 1,780.92 m²
Radius r = a / 2
r = 27.71 / 2 = 13.85 m
Base surface area B = 2(e² - h²)
B = 2(35² - 29²)
= 2(1225 - 841)
= 2(384) = 768 m²
Total surface area A = a√(a² + 4h²) + 2(e² - h²)
A = 768 + 1,780.92 = 2,548.92 m²
∴ Square pyramid side length is 27.71 m, the radius is 13.85 m, height is 29 m, slant height is 13.85 m, the base surface area is 768 m², the lateral surface area is 1,780.92 m², the volume is 7,424 m³, lateral edge length is 35 m, and total surface area is 2,548.92 m².
Example 2: Compute the square pyramid slant height, radius, total surface area, lateral surface area, volume, lateral edge length, base surface area, and total surface area. If the pyramid height is 12 cm, side length is 6 cm.
Solution:
Given that,
Square pyramid height h = 12 cm
Pyramid side length a = 6 cm
Volume V = (1/3)a²h
V = (1/3) * 6² * 12
= (1/3) * 36 * 12 = 432 / 3
= 144 cm³
Lateral Surface Area L = a√(a² + 4h²)
L = 6√(6² + 4*12²)
= 6√(36 + 4*144) = 6√(36 + 576)
= 6√612 = 6 * 24.73 = 148.43 cm²
Base Surface Area B = a²
B = 6² = 36 cm²
Total Surface Area A = L + B = a(a + √(a² + 4h²))
A = 36 + 148.43 = 184.43 cm²
Lateral Edge Length e = √(h² + (1/2)a²)
e = √(12² + (1/2)6²)
= √(144 + (1/2)36)
= √(144 + 18) = √162
= 12.72 cm²
Radius r = a / 2
r = 6 / 2 = 3 cm
Slant Heigh s = √(h² + (1/4)a²)
s = √(12² + (1/4)6²)
= √(144 + (1/4)36)
= √(144 + 9) = √153
= 12.36 cm²
∴ Square pyramid side length is 6 cm, the radius is 3 cm, height is 12 cm, slant height is 12.36 cm, the base surface area is 36 cm², the lateral surface area is 148.43 cm², the volume is 144 cm³, lateral edge length is 12.72 cm², and total surface area is 184.43 cm².
Seek instant help regarding several geometry concepts all at one place Areavolumecalculator.com and clear all your ambiguities easily.
FAQs on Pyramid Calculator
1. What are the properties of a square pyramid?
The square pyramid properties are given here:
Base is square
It has 8 edges, 5 faces, and vertices.
The 4 side faces are triangles.
2. What is the square pyramid face area formula?
Square pyramid face area formula is face area = (a/2)[√((a² / 4) + h²). Where a is the side length, h is the height.
3. Find the total surface area of a regular pyramid having a square base where the length of each edge of the base is equal to 8 m, the slant height of a side is 15 m and the altitude is 18 m?
Perimeter of sqaure is P = 4a = 4 * 8 = 32 m
Area of sqaure A = a² = 8² = 64 m²
Total surface area = ½ * 32 * 15 + 64 = 304 m².
