Polygon Calculator
Do you want to learn about regular polygons? You have reached the correct place. This page contains useful details like formulas, steps, and example problems on regular polygons. You can find the area, perimeter, inradius, circumradius, interior angle, exterior angle of a polygon on the Polygon Calculator page.
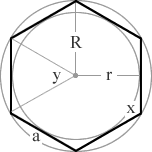
| n | n = 6 sides |
| side length | a = |
| in radius | r = |
| circumradius | R = |
| area | A = |
| perimeter | P = |
| interior angle | x = |
| exterior angle | y = |
Regular Polygon Formulas
A regular polygon is a polygon that has both equiangular and all sides of equal length. Have a look at the simple formulas that are helpful to find inradius, circumradius, area, perimeter, side length interior angle, exterior angle. Get the formulae from the following sections.
- The Formula to Calculate Side Length of a Polygon:
- a = 2r tan(π/n) = 2R sin(π/n)
- Inradius Formula:
- r = (1/2)a cot(π/n) = R cos(π/n)
- Circumradius of a Polygon Formula:
- R = (1/2) a csc(π/n) = r sec(π/n)
- The Formula to Calculate Area of a Polygon:
- A = (1/4)na² cot(π/n) = nr² tan(π/n)
- Polygon Perimeter Formula:
- P = na
- Interior Angle of a Polygon Formula:
- x = ((n-2)π / n) radians = (((n-2)/n) x 180° ) degrees
- Exterior Angle of a Regular Polygon Formula:
- y = (2π / n) radians = (360° / n) degrees
Where,
n is the number of sides of a regular polygon
a is the length of the side of a polygon
r is the inradius
R is the circumradius of a polygon
A is the area of the polygon
P is the perimeter of the polygon
x is the interior angle of a regular polygon
y is the exterior angle of a polygon
What is meant by Regular Polygon?
Polygon is a two-dimensional flat-shaped figure which does not have any curved surface. Regular polygons have equal sides and angle measurement. The polygon with the least number of sides is a triangle and n number of sides is called n-gon. Different shapes of the regular polygons are listed here:
- Trigon (equilateral triangle):
- Number of sides = 3
- Interior angle = (1/3)π = 60°
- Exterior angle = (2/3)π = 120°
- Tetragon (Square):
- Number of sides = 4
- Interior angle = (2/4)π = 90°
- Exterior angle = (2/4)π = 90°
- Pentagon:
- Number of sides = 5
- Interior angle = (3/5)π = 108°
- Exterior angle = (2/5)π = 72°
- Hexagon:
- Number of sides = 6
- Interior angle = (4/6)π = 60°
- Exterior angle = (2/6)π = 120°
- Heptagon:
- Number of sides = 7
- Interior angle = (5/7)π = 128.57°
- Exterior angle = (2/7)π = 51.43°
- Octagon:
- Number of sides = 8
- Interior angle = (6/8)π = 135°
- Exterior angle = (2/8)π = 45°
- Nonagon:
- Number of sides = 9
- Interior angle = (7/9)π = 140°
- Exterior angle = (2/9)π = 40°
- Decagon:
- Number of sides = 10
- Interior angle = (8/10)π = 144°
- Exterior angle = (2/10)π = 36°
- Undecagon:
- Number of sides = 11
- Interior angle = (8/11)π = 147.27°
- Exterior angle = (2/11)π = 32.73°
- Dodecagon:
- Number of sides = 12
- Interior angle = (10/12)π = 150°
- Exterior angle = (2/12)π = 30°
- Tridecagon:
- Number of sides = 13
- Interior angle = (11/13)π = 152.31°
- Exterior angle = (2/13)π = 27.69°
- Tetradecagon:
- Number of sides = 14
- Interior angle = (12/14)π = 154.29°
- Exterior angle = (2/14)π = 25.71°
How to Solve Polygon Area, Perimeter, Angles?
Below given are the easy and simple instructions to calculate the area, perimeter, inradius, side length, exterior angle, interior angle, and circumradius of the polygon. Have a look at them and follow to solve questions effectively.
Inradius:
- Process 1:
- Get the number of sides and the side length of the polygon from the question.
- Divide the π with the number of sides of the polygon.
- Get the cot function of the result.
- Find half of the side length and multiply it with the result obtained in the above step.
- Process 2:
- Get the cos of π/no. of sides and multiply it with the circumradius value.
Side Length:
- Process 1:
- Observe the number of sides and inradius of a polygon.
- Double the inradius.
- Divide π with the number of sides of a polygon.
- Get the tan of the resultant and multiply it with the number obtained in step 2.
- Process 2:
- Note down circumradius and number of sides.
- Double the circumradius.
- Get sin of π/no of sides.
- Multiply those values to check side length.
Circumradius:
- Process 1:
- Make a note of the given side length, the number of sides from the question.
- Get half of the side length.
- Find the cosec of π/no of sides.
- Multiply those two values.
- Process 2:
- Multiply the inradius with the sec of π/no of sides.
Area:
- Process 1:
- Get the (1/4) of the number of sides of a polygon.
- Square the length of the side of a polygon.
- Compute cot function of π/number of sides.
- Multiply the values obtained in the above steps to get the area.
- Process 2:
- Square the inradius, multiply it with the number of sides.
- Evaluate the tan function of π/number of sides.
- Get the product of those values to check the result.
Perimeter:
- Add up all the sides length or multiply the number of sides of the polygon with the side length.
Interior Angle:
- The only thing you need is a number of sides of a polygon.
- Subtract two from the number of sides.
- Multiply it with π/ no. of sides of the polygon to check interior angle in terms of radians.
- Divide the subtracted value by no sides.
- Multiply the result with 180° to get the interior angle in terms of degrees.
Exterior Angle:
- Double the π and divide it by no sides to get an exterior angle in radians.
- Divide 360° by the number of sides of a polygon to check the exterior angle in degrees.
Solved Example Questions
Example 1: Find circumradius, inradius, perimeter, area, exterior angle, interior angle of a regular polygon having 20 sides. The length of each side is 20 m.
Solution:
Given that,
Number of sides of polygon n = 20
Side length a = 20 m
Inradius r = (1/2)a cot(π/n)
= (1/2) * 20 cot(π/20)
= 10 cot(9°)
= 10 * 6.313
= 63.13
Circumradius R = (1/2) a csc(π/n)
= (1/2) 20 cosec(π/20)
= 10 * cosec(9°)
= 10 * 6.41
= 64.1
Area A = (1/4)na² cot(π/n)
= (1/4) * 10 * 20² cot(π/20)
= 2.5 * 400 * cot(9°)
= 1000 * 6.32
= 6320
Perimeter P = na
= 20 * 20
= 400
Interior Angle X = (((n-2)/n) x 180° ) degrees
= ((20 - 2) / 20) x 180°
= (18 / 20) x 180°
= 0.9 x x 180°
= 162°
X = ((n-2)π / n) radians
= ((20 - 2) π / 20)
= (18π/20)
= 0.9 π
= 162 radians
Exterior Angle y = 360° / n
= 360° / 20
= 18°
∴ Polygon area is 6320 m², perimeter is 400 m, circu,radius is 64.1 m, inradius is 63.13 m, interior angle is 162°, exterior angle is 18°.
Example 2: Calculate side length, inradius, circumradius, perimeter, and angles of an undecagon having an area 256 cm²?
Solution:
Given that,
Number of sides of a polygon n = 11
Area of polygon A = 256 cm
Side length a = √((4A) / (n cot(π/n)))
= √((4 * 256) / (11 cot(π/11)))
= √(1024 / (11 * cot(16.36)))
= √(1024 / (11 * 3.406))
= √(1024 / 37.466)
= √27.33
= 5.22
Inradius r = (1/2)a cot(π/n)
= (1/2) * 5.22 cot(π/11)
= 2.61 * cot(16.36)
= 2.61 * 3.406
= 8.88
Circumradius R = r sec(π/n)
= 8.88 * sec(π/11)
= 8.88 * sec(16.36)
= 8.88 * 1.04
= 9.235
Perimeter P = na
= 11 * 5.22
= 57.42
Interior Angle x = ((n - 2)π / n) radians
= (11 - 2)π / 11
= 9π / 11
= 147.27
Exterior angle y = (2π / n)
= 2π / 11
= 32.73
∴ The side length of the undecagon is 5.22 cm, the inradius is 8.88 cm, circumradius is 9.235, the perimeter is 57.42 cm, the interior angle is 147.27, the exterior angle is 32.73.
Areavolumecalculator.com is an advanced geometry education tool where you can learn, practice, and discover topics using our handy calculators.
FAQs on Polygon Calculator
1. How do you find the area of a regular polygon calculator?
The formula to calculate the polygon area using apothem is A = n * a * apothem / 2
Using side length is A = n * a² * cot(π/n) / 4
using perimeter is A = P * apothem / 2.
Where a is the polygon side length
n is the no of sides of a polygon.
2. How many degrees are in a polygon?
A regular polygon is a flat shape where all sides and angles are equal. The formula to find the sum of the measure of the interior angles is (n - 2) * 180°. To get the one interior angle measure divide the sum by the number of sides.
3. What is 1000 sided shape called?
1000 sides polygon is called chiliagon or 1000-gon. The interior angle is (998 * 180°) / 1000 = 179.64°. The exterior angle is 360° / 1000 = 0.36°.
