Parallelogram Calculator
Parallelogram Calculator: Avail free handy calculator tool that calculates the area, corner angles, perimeter, diagonals lengt3h, and side length of a parallelogram. You can find all the details without any hassle by simply providing the side length or any other parameters metrics in the input fields of the calculator. Press on the calculate button to navigate to the output page in a fraction of seconds. Make your calculations much easier and faster with our online tool.
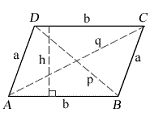
| corner angles A = C = | |
| corner angles B = D = | |
| side a length a = | |
| side b length b = | |
| diagonal length p = | |
| diagonal length q = | |
| height h = | |
| perimeter P = | |
| area K = |
Formulas to Calculate Parallelogram Area, Perimeter
Below given are the formulas that help you to solve the parallelogram area, perimeter, two diagonals length, corner angles.
Area:
- R = base * height = bh
- R = ab sin(A)
- R = ab sin(B)
- R = ½ * p * q sin(A)
Perimeter:
P = 2(a + b)
Height:
- h = a sin(A)
- h = a sin(B)
Corner Angles:
- A = C
- B = D
- A + B = 180° = π radians
for a parallelogram that is not a rectangle or square,
0 < A< 90° (0 < A < π/2),
90° < B < 180° (π/2 < B < π)
Diagonals:
- p = √(a² + b² - 2ab cos(A)) = √( a² + b² + 2ab cos(B) )
- q = √(a² + b² + 2ab cos(A)) = √( a² + b² - 2ab cos(B) )
- p² + q² = 2(a² + b²)
Parallelogram Calculations:
This section is useful to find the unknown parameter of the parallelogram using its sides or diagonals or angles or any others.
- Calculate 3 different corner angles using one angle:
- B = 180° - A C = A D = B
- Calculate height, other three angles using one angle and side length:
- Height h = a sin(A) B = 180° - A C = A D = B
- Calculate side length, 3 angles using height, and one angle:
- Side length a = h / sin(A)
- B = 180° - A C = A D = B
- Calculate other side length using perimeter and one side length:
- b = (P - 2a)/2
- Calculate height using area and one side length:
- Height h = R / b
- Calculate side length using area and height:
- Side length b = R / h
- Calculate corner angles, diagonals, height, perimeter, area uisng two sides and corner angle:
- First diagonal length p = √(a² + b² - 2ab cos(A))
- Second diagonal length q = √(a² + b² + 2ab cos(A))
- Perimeter P = 2(a + b)
- Height h = a sin(A)
- Area R = bh
- B = 180° - A
- C = A
- D = B
- Calculate Corner angles A, B, diagonal q, height h, perimeter P, and Area R using sides length a, b, diagonal p:
- Corner angle A = arccos( (p² - a² - b²) / (-2ab) )
- Diagonal q = √( a² + b² + 2ab cos(A) )
- Height h = a sin(A)
- Perimeter P = 2a + 2b
- Area R = ab sin(A)
- B = 180° - A
- C = A
- D = B
- Calculate corner angles, diagonals, perimeter, area using sides length and height:
- Corner angle A = arcsin(h/a)
- Diagonal p = √( a² + b² - 2ab cos(A) )
- Diagonal q = √( a² + b² + 2ab cos(A) )
- Perimeter P = 2a + 2b
- Area R = ab sin(A)
- B = 180° - A
- C = A
- D = B
Where,
A, B, C, D are the corner angles
R is the area of a parallelogram
a, b are the sides of a parallelogram
p, q are the diagonals of the parallelogram
h is the height
P is the perimeter
Methods to Find Parallelogram Area, Perimeter, Diagonals
Here are the simple and easy methods to compute the parallelogram area, perimeter, height, and diagonals length. Follow them, solve the parallelogram questions speedily.
Area:
- Method 1:
- Get one side length, the height of the parallelogram.
- Multiply side length and height of the parallelogram to get area.
- Method 2:
- Know diagonals length, one angle of a parallelogram.
- Multiply the length of the diagonal and divide it by 2.
- Multiply the obtained result with a sine function of angle to check the area.
- Method 3:
- Find parallelogram sides length, one corner angle from the question.
- Multiply the length of the parallel sides.
- Get the product and multiply it with the sine of the corner angle.
Perimeter:
- Get sides of the parallelogram.
- Add up all the sides to find a perimeter.
Height:
- Multiply side length with the sine function of one corner angle to get the height.
Diagonals Length:
- Substitute values in the shorter diagonal, longer diagonal formulas.
- Perform the required math operations to check diagonals lengths.
Corner Angles:
- The sum of the adjacent corner angles is always 180°.
- Opposite corner angles measure equal.
Methods to Find Parallelogram Area, Perimeter, Diagonals
Here are the simple and easy methods to compute the parallelogram area, perimeter, height, and diagonals length. Follow them, solve the parallelogram questions speedily.
Area:
- Method 1:
- Get one side length, the height of the parallelogram.
- Multiply side length and height of the parallelogram to get area.
- Method 2:
- Know diagonals length, one angle of a parallelogram.
- Multiply the length of the diagonal and divide it by 2.
- Multiply the obtained result with a sine function of angle to check the area.
- Method 3:
- Find parallelogram sides length, one corner angle from the question.
- Multiply the length of the parallel sides.
- Get the product and multiply it with the sine of the corner angle.
Perimeter:
- Get sides of the parallelogram.
- Add up all the sides to find a perimeter.
Height:
- Multiply side length with the sine function of one corner angle to get the height.
Diagonals Length:
- Substitute values in the shorter diagonal, longer diagonal formulas.
- Perform the required math operations to check diagonals lengths.
Corner Angles:
- The sum of the adjacent corner angles is always 180°.
- Opposite corner angles measure equal.
Examples on Parallelogram
Example 1: Find three corner angles, diagonals, perimeter, area, height? If parallelogram sides are 3 cm, 7 cm and angle is 75°.
Solution:
Given that,
Parallelogram sides a = 3 cm, b = 7 cm
Corner angle A = 75°
Shorter diagonal length p = √(a² + b² - 2ab cos(A))
= √(3² + 7² - 2 * 3 * 7 cos(75°))
= √(9 + 49 - 42 * 0.258)
= √(58 - 10.83)
= √(47.17)
= 6.86
Longer diagonal length q = √(a² + b² + 2ab cos(A))
= √(3² + 7² + 2 * 3 * 7 cos(75°))
= √(9 + 49 + 42 * 0.258)
= √(58 + 10.83)
= √(68.83)
= 8.29
Perimeter P = 2(a + b)
= 2(3 + 7)
= 2(10)
= 20
Height h = a sin(A)
= 3 * sin(75°)
= 3 * 0.965
= 2.895
Area of parallelogram = bh
= 7 * 2.895
= 20.265
Corner angles
B = 180° - A
= 180° - 75°
= 105°
C = A
= 75°
D = B
= 105°
∴ Area is 20.26 cm², perimeter is 20 cm, diagonals are p is 6.86 cm, q is 8.29 cm, height is 2.895 cm, corner angles B is 105°, C is 75°, D is 105°.
Example 2: Compute corner angles, height, area, perimeter, a side length of a parallelogram? If diagonals are 59 cm, 50 cm and the side length is 12 cm.
Solution:
Given that,
Diagoanls p = 59 cm, q = 50 cm
Side length b = 12 cm
Other side length a = √( (p² + q² - 2b²) / 2 )
= √((59² + 50² - 2(12)²) / 2)
= √((3481 + 2500 - 2(144)) / 2)
= √((5981 - 288) / 2)
= √((5693) / 2)
= √(2846.5)
= 53.35
Corner angle
A = arccos( (q² - a² - b²) / (2ab) )
= arccos((50² - 53.35² - 12²) / (2 * 53.35 * 12))
= arccos((2500 - 2,846.2 - 144) / (1280.4))
= arccos((2500 - 2990.2) / 1280.4)
= arccos((-490.2) / 1280.4)
= arccos(0.382)
= 112.52°
C = 112.52°
B = 180° - A
= 180° - 112.52°
= 67.48°
Height h = a sin(A)
= 53.35 * sin(112.52°)
= 53.35 * 0.923
= 49.242
Perimeter P = 2a + 2b
= 2(53.35 + 12)
= 2(65.35)
= 130.7
Area R = ab sin(A)
= 53.35 * 12 * sin(112.52°)
= 640.2 * 0.923
= 591.39
∴ Perimeter of the parallelogram is 130.7 cm, area is 591.39 cm², height is 49.2 cm, diagonals are 59 cm, 50 cm, side length is 53.35 cm, angles are 112.5°, 67.47°.
Check our website Areavolumecalculator.com to get the various calculator concepts that help you to solve all your lengthy math calculations more efficiently and learn the concept easily by referring to the detailed steps.
Frequently Asked Questions on Parallelogram Calculator
1. What is Meant by Parallelogram?
A parallelogram is a simple quadrilateral with two pairs of parallel sides. It is a two-dimensional geometric shape where parallel sides are in equal length. Also, the interior opposite angles of a parallelogram are equal in measure. The sum of adjacent angles of a parallelogram is equal to 180 degrees. The parallelogram has 4 sides and 4 vertices.
2. What are the properties of a parallelogram?
Opposite sides and angles are congruent.
Consecutive angles are supplementary.
Diagonals bisect each other.
Each diagonal divides parallelogram into two triangles.
3. What is the formula of the diagonal of a parallelogram?
Let us say the diagonals are p, q and sides are a, b and A, b are corner angles.
p = √(a² + b² - 2ab cos(A)) = √( a² + b² + 2ab cos(B) )
q = √(a² + b² + 2ab cos(A)) = √( a² + b² - 2ab cos(B) )
p┬▓ + q┬▓ = 2(a┬▓ + b┬▓)
4. Is diagonal of parallelogram equal?
No, diagonals of a parallelogram are not in equal length, because the sides are parallel to each other. The diagonals bisect each other at the center of the parallelogram.
