Isosceles Triangle Calculator
Isosceles Triangle is a polygon having three sides. Two sides and angles of an isosceles triangle measure equal. The other side of the triangle is called the base and another angle is called the base angles.
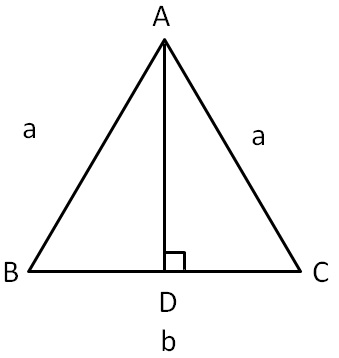

| a = | |
| b = | |
| c = | |
| P = | |
| s = | |
| K = | |
| ha = | |
| hb = | |
| hc = |
Isosceles Triangle Formulas
Isosceles Triangle is a triangle that has two sides of equal length. In some cases, it has exactly two sides of equal length and otherwise having at least two sides of equal length. The two equal sides are called the legs and the third side is called the base of the triangle. The other dimensions of the triangle like altitude, area, the perimeter can be calculated by using the simple formulas mentioned below.
Altitude is a line drawn from one vertex of the triangle to the midpoint of its opposite side. The height of an isosceles triangle divides it into two right-angled triangles.
- Sides of Isosceles Triangle: a = c
- Angles of Isosceles Triangle: A = C
- Altitudes of Isosceles Triangle: ha = hc = alt, hb = h
- Area of an Isosceles Triangle Formula:
- Area K = ½ * b * h
- Area K = (1/4) * b * √( 4 * a² - b² )
- Area K = (1/2) * a * b * sin(base_angle) = (1/2) * a² * sin(vertex_angle)
- Perimeter of an Iosceles Triangle Formula:
- Perimeter P = a + a + b = 2a + b
- Semiperimeter of an Isosceles Triangle Formula:
- Semiperimeter s = (a + b + c) / 2 = a + (b/2)
- Altitude of Isosceles Triangle Formula:
- alt = (b/2a) * √(4a² - b²)
- Height of an Isosceles Triangle Formula:
- h = (1/2) * √(4a² - b²)
- Base angle of an Isosceles Triangle Formula:
- Base angle sin(α) = h / a
- Vetex angle of an Isosceles Triangle Formula:
- Vertex angle sin(β) = b/ 2a
Isosceles Triangle Calculations:
- If the height of the triangle, base length are known, then
- Area K = ½ * b * h
- Side length a = √(h² + (b² / 4))
- Perimeter P = 2√(h² + (b² / 4)) + b
- Seimeperimeter s = √(h² + (b² / 4)) + (b/2)
- Base angle sin(α) = h / √(h² + (b² / 4))
- Vertex angle sin(β) = b/ 2√(h² + (b² / 4))
- Altitude alt = (b/2√(h² + (b² / 4))) * √(4h²)
- If the side length and base of the triangle is known, then
- Perimeter P = 2a + b
- Area K = (1/4) * b * √( 4 * a² - b² )
- Seimeperimeter s = a + (b/2)
- Height h = (1/2) * √(4a² - b²)
- Base angle sin(α) = h / a
- Vertex angle sin(β) = b/ 2a
- Altitude alt = (b/2a) * √(4a² - b²)
- If base, vertex angles, the side length of the triangle are given, then
- Base length b = 2a * sin(β)
- Height h = a * sin(α)
- Area K = ½ * b * h
- Perimeter P = 2a + b
- Seimeperimeter s = a + (b/2)
- Altitude alt = (b/2a) * √(4a² - b²)
Where,
a is the side length.
b is the base length is the height
A, B, C are the vertices
alt is the altitude of the triangle
P is the triangle perimeter
s is the semiperimeter of the triangle
K is the isosceles triangle area
α is the base angle
β is the vertex angle
Steps to Find Measures of an Isosceles Triangle
In geometry, the triangle is an important topic. An isosceles triangle is a type of triangle having 2 sides of equal length. Follow these simple guidelines to find the altitude, height, area, perimeter, semiperimeter, side length, base length, base angle, and vertex angle.
Isosceles Triangle Area:
- Process 1:
- Get the base, height of the isosceles triangle.
- Multiply base, height.
- Divide the result by 2 to check the area.
- Process 2:
- Make a note of the side length, the base of the triangle from the question.
- Square the side length, base.
- Multiply the square of side length by 4.
- Subtract the result from the square of base and apply the square root to it.
- Divide the base by 4 and multiply it with the result of the above step.
Isosceles Triangle Perimeter:
- Get all three sides of the triangle.
- Add up all the sides to get the perimeter.
Isosceles Triangle Semiperimeter:
- Check out all three sides of the triangle.
- Add up the sides and divide the sum by 2 to find semiperimeter.
Isosceles Triangle Altitude:
- Note downside length, the base of an isosceles triangle.
- Multiply the square of side length with 4 and subtract it from the square of the base.
- Apply the square root function to the result.
- Divide the base by 2 times of side length.
- Multiply the result of step 3, step 4 to get altitude.
Isosceles Triangle Height:
- Check isosceles triangle base, side length.
- Square the common side length and base length.
- Multiply the side length with 4 and subtract it from the base square.
- Apply square root to the subtracted value.
- Divide the result by 2 to get the height of a triangle.
Isosceles Triangle Base Angle:
- Get height, a side length of the triangle.
- Divide the height by side length to get the sine function of the base angle.
Isosceles Triangle Vetex Angle:
- Check out the base length and side length from the question.
- Divide the base length by twice of side length.
- The obtained value is the sine function of the vertex angle.
Example Questions on Isosceles Triangles
Example 1: Find the unknown measures of an isosceles triangle? If the side length and base length of the triangle is 5 cm, 8 cm respectively.²
Solution:
Given that,
The side length of an isosceles triangle a = 5 cm
The base length of an isosceles triangle b = 8 cm
Isosceles Triangle Area K = (1/4) * b * √( 4 * a² - b² )
= (1/4) * 8 * √( 4 * 5² - 8² )
= (1/4) * 8 * √( 4 * 25 - 64 )
= (1/4) * 8 * √( 100 - 64 )
= (1/4) * 8 * √(36)
= (1/4) * 8 * 6
= (1/4) * 48
= 12 cm²
Isosceles Triangle Height h = (1/2) * √(4a² - b²)
= (1/2) * √( 4 * 5² - 8² )
= (1/2) * √( 4 * 25 - 64 )
= (1/2) * √( 100 - 64 )
= (1/2) * √(36)
= (1/2) * 6
= 3 cm
Isosceles Triangle Perimeter P = 2a + b
= 2 * 5 + 8
= 10 + 8
= 18 cm
Isosceles Triangle Seimeperimeter s = a + (b/2)
= 5 + (8/2)
= 5 + 4
= 9 cm
Isosceles Triangle Altitude alt = (b/2a) * √(4a² - b²)
= (8/(2 * 5)) * √( 4 * 5² - 8² )
= (8/(2 * 5)) * √( 4 * 25 - 64 )
= (8/(2 * 5)) * √( 100 - 64 )
= (8/(2 * 5)) * √(36)
= (8/(2 * 5)) * 6
= (8/10) * 6
= 48 / 10
= 4.8 cm
Isosceles Triangle Base angle sin(α) = h / a
= 3 / 5
= 0.6
α = 36.9°
Isosceles Triangle Vertex angle sin(β) = b/ 2a
= 8/(2 * 5)
= 8 / 10
= 0.8
β = 106.3°
∴ Isosceles triangle base length is 8 cm, side length is 5 cm, the area is 12 cm², the perimeter is 3 cm, semiperimeter is 9 cm, altitude is 4.8 cm, the base angle is 36.9° vertex angle is 106.3°.
Example 2: If an isosceles triangle is having a height of 10 m and a base length of 6 m, then compute the triangle area, perimeter, semiperimeter, side length, altitude, vertex angle, and base angle?
Solution:
Given that,
Height of an isosceles triangle h = 10 m
base length b = 6 m
Isosceles Triangle Side length a = √(h² + (b² / 4))
= √(10² + (6² / 4))
= √(100 + (36 / 4))
= √(100 + 9)
= √(109)
= 10.44 m
Isosceles Triangle Perimeter P = 2√(h² + (b² / 4)) + b
= 2 * √(10² + (6² / 4)) + 6
= 2 * √(100 + (36 / 4)) + 6
= 2 * √(100 + 9) + 6
= 2 * √(109) + 6
= 2 * 10.44 + 6
= 20.88 + 6
= 26.88 m
Isosceles Triangle Seimeperimeter s = √(h² + (b² / 4)) + (b/2)
= √(10² + (6² / 4)) + (6/2)
= √(100 + (36 / 4)) + 3
= √(100 + 9) + 3
= √(109) + 3
= 10.44 + 3
= 13.44 m
Isosceles Triangle Base angle sin(α) = h / √(h² + (b² / 4))
= 10 / √(10² + (6² / 4))
= 10 / √(100 + (36 / 4))
= 10 / √(100 + 9)
= 10 / √(109)
= 10 / 10.44
= 0.957
= 73.13°
Isosceles Triangle Vertex angle sin(β) = b/ 2√(h² + (b² / 4))
= 6 / 2 * √(10² + (6² / 4)) + 6
= 6 / 2 * √(100 + (36 / 4)) + 6
= 6 / 2 * √(100 + 9) + 6
= 6 / 2 * √(109) + 6
= 6 / 2 * 10.44 + 6
= 6 / 20.88 + 6
= 6 / 26.88
= 0.223
= 12.88°
Isosceles Triangle Altitude alt = (b/2√(h² + (b² / 4))) * √(4h²)
= (6 / 2 * √(10² + (6² / 4)) + 6) * √(4 * 10²)
= (6 / 2 * √(100 + (36 / 4)) + 6) * √(4 * 100)
= (6 / 2 * √(100 + 9) + 6) * √(400)
= (6 / 2 * √(109) + 6) * 20
= (6 / 2 * 10.44 + 6) * 20
= (6 / 20.88 + 6) * 20
= (6 / 26.88) * 20
= 0.223 * 20
= 4.464 m
Isosceles Triangle Area K = ½ * b * h
= ½ * 6 * 10
= 60 / 2
= 30 m²
∴ Isosceles triangle base length is 6 cm, side length is 10.44 m, the area is 30 m², the perimeter is 26.88 m, semiperimeter is 13.44 m, altitude is 4.464 m, the base angle is 73.13° vertex angle is 12.88°.
Make use of these free online calculator tools available for various geometry topics all at one place on Areavolumecalculator.com and clear all your queries while doing assignments and homework.
FAQs on Isosceles Triangle
1. What are the properties of an isosceles triangle?
- Two sides are congruent to each other.
- The third side is not equal to the other two sides called the base of the triangle.
- The two angles opposite to the equal sides are congruent to each other.
- An angle that is not congruent is called an apex angle.
- Altitude from the apex divides the base into two equal parts is called height.
2. How do you calculate an isosceles triangle?
For an isosceles triangle, two sides are equal (a = c) and angles are also equal (A = C). Two altitudes of an isosceles triangle are equal ha = hb. The perimeter of the triangle is the sum of all three sides. Semiperimeter is obtained by dividing the perimeter into half. The area is the space occupied by the isosceles triangle.
3. What are the examples of an isosceles triangle?
The examples of an isosceles triangle are isosceles right triangle, golden triangle, and faces of bipyramids and certain Catalan solids.
4. How do you use the isosceles triangle calculator?
You can calculate the height, semiperimeter, perimeter, area, base angle, vertex angle, the altitude of an isosceles triangle by giving the side length, base length in the specified input sections of the calculator. Tap on the calculate button to get the exact values as soon as possible.
