Cube Calculator
Cube is a three-dimensional geometric figure that has 6 faces, 8 vertices, and 12 edges. It is a regular hexahedron. The SI unit of the cube is cubic units. All faces and angles measure equal dimensions.
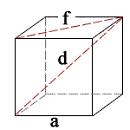
| side length | a = |
| face diagonal | f = |
| solid diagonal | d = |
| surface area | S = |
| volume | V = |
Cube Calculator: Having knowledge of geometry concepts will make you strong in attempting all exams. Here we are providing each and every step that helps you to calculate the cube face diagonal, side length, solid diagonal, surface area, and volume. We have also given the example problems for a better understanding of the concept. Get the simple formulas to solve the missing side length and other parameters of a cube easily.
Take advantage of the free online Cube Calculator to solve side length, face diagonal, solid diagonal, volume, and surface area. Enter known values in the specified input boxes and press the calculate button. It will generate the output in a fraction of seconds easily.
Formulas to Calculate Cube Diagonal, Surface Area, Volume
In geometry, a cube is a three-dimensional figure bounded by 6 square sides. To calculate the volume, surface area, diagonal, and side length of a cube you must follow the simple formulas mentioned below. Using these formulas you can calculate the unknown measures effortlessly.
Cube Calculations
- The Volume of a Cube Formula:
- Volume V = a³
- Surface Area of a Cube Formula:
- Surface Area S = 6a²
- Face Diagonal of a Cube Formula:
- f² = a² + a²
- f² = 2a²
- f = a√2
- Diagonal of the Solid Cube Formula:
- d² = a²+ f²
- d² = a² + 2a² = 3a²
- d = a√3
- If the face diagonal of a cube is given, then
- Side length a = f / √2
- Volume V = f³ / 2√2
- Solid Diagonal d = f√3 / √2
- Surface Area S = 3f²
- If a solid diagonal of the cube is given, then
- Side length a = d / √3
- Surface area S = 2d²
- Volume V = d³ / 3√3
- Face diagonal length f = d√2 / √3
- If the Volume of a cube is known, then
- Side length a = ∛V
- Face diagonal length f = a√2
- Solid Diagonal length d = a√3
- Surface Area S = 6a²
- If the surface area of the cube is given, then
- Side length a = √( S / 6 )
- Volume V = [√( S / 6 )]³
- Solid diagonal d = √( S / 2 )
- Face diagonal f = √( S / 3 )
Where, a is the cube side length
V is volume
S is the surface area
f is the face diagonal length of a cube
d is the diagonal of a solid cube
Steps for Calculating Cube Surface Area, Volume, Diagonal
Follow these guidelines while solving the cube volume, surface area, solid diagonal, face diagonal, and unknown side length.
Cube Volume:
- Get the cube side length.
- Apply cube function to the length to check volume.
Cube Face Diagonal:
- Make a note of the side length of the cube from the question.
- Multiply the side length by the square root of 2 to know the face diagonal.
Cube Solid Diagonal:
- Find the cube side length.
- Multiply the side length with a square root of 3 to get a solid diagonal length.
Cube Surface Area:
- Get side length of the cube.
- Square the side length.
- Multiply the squared value with 6 to check surface area.
Cube Side Length:
- Process 1:
- Note down the cube volume.
- Apply cube root of volume to get the side length.
- Process 2:
- Get the surface area of the cube from the question.
- Divide the surface area by 6.
- Apply square root to the result to know side length.
- Process 3:
- Check out the face diagonal length of a cube.
- Divide the face diagonal value by a square root of 2 to know side length.
- Process 4:
- Have a look at the diagonal of a solid cube.
- Divide the diagonal length by a square root of 3.
- The obtained result is called its side length.
Examples Questions of Cube
Example 1: If the cube volume is 729 m³. Calculate the cube face diagonal, solid diagonal, side length, and surface area?
Solution:
Given that,
Cube volume V = 729 m³
Side length a = ∛V
a = ∛729
= Γê¢9³ = 9 m
Face diagonal length f = a√2
f = 9 * √2
= 9 * 1.414 = 12.72 m
Solid Diagonal length d = a√3
d = 9 * √3
= 9 * 1.732 = 15.58 m
Surface Area S = 6a²
S = 6 * 9² = 6 * 9 * 9
= 6 * 81 = 486 m²
∴ Cube side length is 9 m, surface area is 486 m², volume is 729 m³, face diagonal length is 12.72 m, and solid diagonal length is 15.58 m.
Example 2: Compute volume, surface area, side length, solid diagonal length of a cube. If the cube face diagonal is 26 cm.
Solution:
Given that,
Cube face diagonal length f = 26 cm
Surface Area Formula is
Surface Area S = 3f²
S = 3 * 26²
= 3 * 26 * 26 = 2,028 cm²
Side length formula is
Side length a = f / √2
a = 26 / √2
= 26 / 1.414 = 18.38 cm
Volume formula is
Volume V = f³ / 2√2
V = 26³ / 2√2
= 17,576 / 2√2
= 17,576 / (2 * 1.414)
= 17,576 / 2.828 = 6,214.99 cm³
Solid Diagonal d = f√3 / √2
d = (26 * √3) / √2
= (26 * 1.732) / 1.414
= 45.03 / 1.44 = 31.27 cm
∴ The cube face diagonal length is 26 cm, side length is 18.38 cm, the surface area is 2,028 cm², solid diagonal length is 31.27 cm, and volume is 6,214.99 cm³.
At Areavolumecalculator.com, you will find various concepts calculators like cube, square, perimeter, cylinder, and many more that assist you to make your calculations quickly and simply.
Frequently Asked Questions on Cube Calculator
1. How do you calculate cube weight?
The simple formula to find the cube weight is side length³ * mean density. So, collect the mean density and side length of the cube. Find the cube of side length and multiply it with mean density to get cube weight value.
2. What is the volume of a cube?
Cube volume is nothing but the amount of space occupied by an object or substance. The basic volume formula is the multiplication of length, width, and height. The cube volume formula is side length³.
3. Solve cube space diagonal and edge measurements?
Space diagonal of a cube is the product of side length or edge and the square root of 3. We have different ways to define the edge. Cube edge in terms of space diagonal is diagonal by the square root of 3, in terms of volume is the cube root of the volume.
4. Find surface area, volume, space diagonal of a cube having side length 4.6 mm?
Surface Area S = 6a²
S = 6 * 4.6² = 6 * 21.16 = 126.96 mm²
Volume V = a³
V = 4.6³ = 4.6 * 4.6 * 4.6 = 97.33 mm³
Space diagonal d = a√3
d = 4.6 * √3 = 4.6 * 1.732 = 7.967 mm