Conical Frustum Calculator
The frustum is the portion of a solid that lies between two parallel planes. The conical frustum is created by cutting the top of a circular cone. Conical Frustum Calculator is a free online tool that computes the radius, volume, height, surface area, and slant height of a conical frustum in just a few seconds. Simply, enter the known parameters in the input boxes and tap on the calculate button to check the result in a blink of an eye.
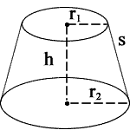
| radius r1 | r1 = |
| radius r2 | r2 = |
| height | h = |
| slant height | s = |
| volume | V = |
| lateral surface area | L = |
| top surface area | T = |
| base surface area | B = |
| total surface area | A = |
Conical Frustum Formulas
The simple formulas to compute the conical frustum height, slant height, radius, surface area, and volume are given here. Have a look at them and follow them when finding the unknown measures. These are the conical frustum formulas in terms of both circles radius and height.
- The Volume of a Conical Frustum Formula:
- Volume V = (1/3) * π * h * (r² + R² + (r * R))
- Lateral Surface Area of a Conical Frustum Formula:
- Lateral Surface Area L = π * (r + R) * s = π * (r + R) * √(r - R)² + h²)
- Top Surface Area of a Conical Frustum Formula:
- Top Surface Area T = πr²
- Base Surface Area of a Conical Frustum Formula:
- Base Surface Area B = πR²
- Total Surface Area of a Conical Frustum Formula:
- Total Surface Area A = π * (r² + R² + (r + R) * s) = π * [ r² + R² + (r + R) * √((r - R)² + h²) ]
- Slant Height of a Conical Frustum Formula:
- Slant Height s = √((r - R)² + h²)
Conical Frustum Calculations:
These formulas are helpful to calculate the unknown measures easily.
- If you know lateral surface area of the frustum, and two circles radii, then
- Slant height s = L / (π * (r + R))
- Height h = √(s² - (r - R)²)
- Volume V = (1/3) * π * √(s² - (r - R)²) * (r² + R² + (r * R))
- Top surface Area T = πr²
- Bottom surface Area B = πR²
- Total Surface Area A = L + B + T = L + πR² + πr²
- If radius of top, bottom circles and volume of frustum are given, then
- Height h = (3 * V) / (π * (r² + R² + (r * R)))
- Slant Height s = √((r - R)² + (3 * V) / (π * (r² + R² + (r * R)))²)
- Top Surface Area T = πr²
- Base Surface Area B = = πR²
- Lateral Surface Area L = π * (r + R) * s
- Total Surface Area A = T + B + L
- If slant height, radius of both circles are given, then
- Height h = √(s² - (r - R)²)
- Volume V = (1/3) * π * h * (r² + R² + (r * R))
- Base Surface Area B = πR²
- Lateral Surface Area L = π * (r + R) * s
- Total Surface Area A = π * (r² + R² + (r + R) * s)
- If total surface area, radius of circles are known, then
- Slant height s = [A/π - r² - R²] / (r + R)
- h = √(s² - (r - R)²)
- Volume V = (1/3) * π *√(s² - (r - R)²) * (r² + R² + (r * R))
- If radius of the top and bottom circles and height of the srustm are given, then
- Lateral Surface Area L = π * (r + R) * s = π * (r + R) * √(r - R)² + h²)
- Slant Height s = √((r - R)² + h²)
- Volume V = (1/3) * π * h * (r² + R² + (r * R))
- Top Surface Area T = πr²
- Base Surface Area B = πR²
- Total Surface Area A = π * (r² + R² + (r + R) * s) = π * [ r² + R² + (r + R) * √((r - R)² + h²) ]
Where,
r is the radius of the top circle
R is the radius of the bottom circle
h is the frustum height
V is volume
L is the frustum lateral surface area
T is the top surface area
B is the bottom surface area
A is the conical frustum total surface area
How to Find Conical Frustum Area, Slant Height, Volume?
To calculate the conical frustum surface area, slant height, and volume go through the simple steps provided below.
Conical Frustum Slant Height:
- Process 1:
- Get radius of both circles and the height of the frustum.
- Subtract those radii and square the value.
- Add a square of height to the result.
- Apply square root to the obtained answer to find slant height.
- Process 2:
- Find lateral surface area, radii of the circles.
- Add radius of circles, multiply sum with π.
- Divide lateral surface area by the output to obtain slant height.
- Process 3:
- Observe total surface area, 2 radii of the frustum.
- Divide the total surface area by π.
- Subtract the squares of the top, bottom circle radius, result.
- Divide the obtained value by the sum of radii to get slant height.
Conical Frustum Top Surface Area:
- Make a note of the radius of the top circle.
- Square the radius and multiply π with it to check the top surface area.
Conical Frustum Volume:
- Check out the height, radius of the top and bottom circles of the frustum.
- Square the top, bottom circles radius and find the product of two radii.
- Add those squares and product.
- Divide the height by 3, multiply the result with π.
- Multiply the values obtained from step 3, step 4 to check volume.
Conical Frustum Base Surface Area:
- Note down the frustum base circle radius.
- Square the radius, multiply π with it to find the base surface area.
Conical Frustum Total Surface Area:
- Get the height, radius of two circles from the question.
- Calculate the lateral, base, top surface areas.
- Add those values to check the total surface area.
Conical Frustum Lateral Surface Area:
- Process 1:
- Check slant height, radii of the top, bottom frustum.
- Add those radii and multiply it with π, slant height to check lateral surface area.
- Process 2:
- Get radii, the height of the frustum from the question.
- Compute the slant height using the known details.
- Multiply the obtained slant height with the sum of radii and π.
Conical Frustum Height:
- Process 1:
- Check out the slant height, radius of the circles.
- Subtract those circles radius from one another and square the value.
- Subtract the result of the above step from the slant height square.
- Apply square root to the answer to find frustum height.
- Process 2:
- Make a note of the volume, radii of two circles.
- Square each radius and multiply the radii.
- Add up those values and multiply with π.
- Divide thrice of volume by the result to check the height.
Conical Frustum Solved Example Questions
Example 1: If the conical frustum total surface area is 1850 m², diameters of the top, base circles are 20 m, 24 m. Find the frustum volume, height, slant height, base surface area, top surface area, and lateral surface area?
Solution:
Given that,
Conical Frustum total Surface Area A = 1850 m²
Diameter of top circle d = 20 m
Radius of top circle r = d / 2 = 20 / 2 = 10 m
Diameter of bottom circle D = 24 m
Radius of bottom circle R = D / 2 = 24 / 2 = 12 m
Slant height formula is s = [A/π - r² - R²] / (r + R)
s = [1850 /3.14 - 10² - 12²] / (10 + 12)
= [589.17 - 100 - 144] / (22)
= [589.17 - 244] / 22
= 345.17 / 22 = 15.689 m
Height h = √(s² - (r - R)²)
By substituting the values
h = √(15.689² - (10 - 12)²)
= √(246.164 - (-2)²)
= √(246.164 - 4)
= √242.164 = 15.56 m
Volume formula is
Volume V = (1/3) * π * √(s² - (r - R)²) * (r² + R² + (r * R))
V = (1/3) * π * √(15.689² - (10 - 12)²) * (10² + 12² + (10 * 12))
= (1/3) * π * √(246.164 - (-2)²) * (100 + 144 + (120))
= (1/3) * π * √(246.164 - 4) * (364)
= (1/3) * π * √242.164 * 364
= 121.33 * π * 15.56
= 1,887.94π
= 1,887.94 * 3.14 = 5,928.152 m³
Top Surface Area of frustum formula is T = πr²
T = π * 10²
= 100π = 100 * 3.14 = 314 m²
Base Surface Area B = πR²
B = π * 12²
= π * 144 = 144 * 3.14 = 452.16 m²
Lateral Surface Area L = π * (r + R) * s
L = π * (10 + 12) * 15.689
= π * 22 * 15.689 = 345.158π
= 345.158 * 3.14 = 1,083.796 m²
∴ Conical frustum lateral surface area is 1,083.796 m², top surface area is 314 m², base surface area is 452.16 m², total surface area is 1850 m², top circle radius is 10 m, base circle radius 12 m, volume is 5,928.152 m³, height is 15.56 m, and slant height is 15.689 m.
Example 2: Solve conical frustum height, total surface area, and volume. If the frustum radii are 7 cm, 15 cm and slant height is 13.6 cm.
Solution:
Given that,
Conical frustum top radius is r = 7 cm
Base radius is R = 15 cm
Slant height s = 13.6 cm
Height of the conical frustum formula is
h = √(s² - (r - R)²)
h = √(13.6² - (7 - 15)²)
= √(185 - (-8)²)
= √(185 - 64)
= √(121) = 11
Volume V = (1/3) * π * h * (r² + R² + (r * R))
V = (1/3) * π * 11 * (7² + 15² + (7 * 15))
= (1/3) * π * 11 * (49 + 225 + 85)
= (1/3) * π * 11 * 359
= (1/3) * π * 3949 = 1,316.33π
= 1,316.33 * 3.14 = 4,133.28 cm³
Lateral Surface Area L = π * (r + R) * √(r - R)² + h²)
L = π * (r + R) * √(r - R)² + h²)
= π * (7 + 15) * √(7 - 15)² + 11²)
= π * (22) * √(-8)² + 11²)
= π * 22 * √64 + 121)
= π * 22 * √185
= π * 22 * 13.6 = 299.23 * π
= 299.23 * 3.14
= 939.58 cm²
Top Surface Area T = πr²
T = π * 7²
= 49π = 49 * 3.14
= 153.86 cm²
Base Surface Area B = πR²
B = π * 15²
= 225π = 225 * 3.14
= 706.5 cm²
Total Surface Area A = π * (r² + R² + (r + R) * s)
= π * (7² + 15² + (7 + 15) * 13.6)
= π * (49 + 225 + 22 * 13.6)
= π * (49 + 225 + 299.2)
= π * 573.2 = 573.2 * 3.14 = 1,799.84 cm²
∴ Conical frustum raddi are 7 cm, 15 cm, slant height is 13.6 cm, height is 11 cm, volume is 4,133.28 cm³, top surface area is 153.86 cm², lateral surface area is 939.58 cm², base surface area is 706.5 cm², and total surface area is 1,799.84 cm².
Take the help of our website Areavolumecalculator.com and learn various difficult geometry concepts that never seemed to understand in a simple way using free tools available.
FAQs on Conical Frustum Calculator
1. What is the formula of conical frustum?
The conical frustum volume, surface area formulas in terms of radius and height are as follows:
Volume V = = (1/3) * π * height * (topradius² + baseradius² + (topradius * baseradius))
Total Surface Area = π * [ topradius² + baseradius² + (topradius + baseradius) * √((topradius - baseradius)² + height²) ]
2. What is the slant height of a frustum?
The slant height of a conical frustum is the distance measured along the lateral face from the base to the top. The formula to calculate the slant height is √((topradius - baseradius)² + height²)
3. What is a conical frustum?
A conical frustum is the part of a cone when it is cut by a plane into two parts. the upper part which is having an apex remains the same but the lower part is called a frustum.
4. What is the lateral surface area of a conical frustum?
The lateral surface area is nothing but the curved surface area. It is obtained by multiplying π, slant height, and difference of radii. Formula is π * slantheight (baseradius - topradius).
