Cone Calculator
Cone is a three-dimensional geometric figure having a circular base joined to a point by the curved side. The pointed end of the cone is called the apex, the flat surface is called the base of the cone.
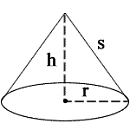
| radius | r = |
| side length | h = |
| slant height | s = |
| volume | V = |
| lateral surface area | L = |
| base surface area | B = |
| total surface area | A = |
| In Terms of Pi π | |
| volume | V = |
| lateral surface area | L = |
| base surface area | B = |
| total surface area | A = |
Circular Cone Formulas
The basic formulas to compute the surface area, volume, height, radius, and slant height of a cone are mentioned here.
- Volume of a Cone Formula:
- Volume V = (1/3)πr²h
- Slant height of a Cone Formula:
- Slant height s = √(r² + h²)
- Lateral Surface Area of a Cone Formula:
- Lateral Surface Area L = πrs = πr√(r² + h²)
- Base surface area of a Cone Formula:
- Base Surface Area B = πr²
- Total Surface Area of a Cone Formula:
- Total Surface Area A = L + B
- = πrs + πr² = πr(s + r) = πr(r + √(r² + h²))
Cone Calculations:
Make use of these additional formulas to know the unknown parameters of a cone easily with lesser calculations.
- If the radius, slant height of a cone are known, then
- Height h = √(s² - r²)
- Volume V = (1/3)πr²(√(s2 - r²))
- Lateral Surface Area L = πrs
- Base Surface Area B = πr²
- Total Surface Area A = πrs + πr²
- If the radius, lateral surface area of the cone are known, then
- Slant height s = L / (πr)
- Height h = √(s² - r²)
- Volume V = (1/3)πr²h
- Base Surface Area B = πr²
- Total Surface Area A = L + πr²
- If the height, slant height of a cone are known, then
- Radius r = √(s² - h²)
- Lateral Surface Area L = πrs = πr√(r² + h²)
- Volume V = (1/3)πr²h
- Base Surface Area B = πr²
- Total Surface Area A = L + B = πrs + πr²
- If cone radius, the volume of a cone are given, then
- Height h = (3 * v) / (πr2)
- Slant Height s = √(r² + h²)
- Lateral Surface Area L = πrs = πr√(r² + h²)
- Base Surface Area B = πr²
- Total Surface Area A = L + B = πrs + πr²
- If the radius and total surface area of a cone are given, then
- Slant height s = [A - (πr2)] / (πr)
- Height h = √(s2 - r2)
- Volume V = (1/3)πr²h
- If volume, the height of a cone are given, then
- Rdaius r = √[ (3 * v) / (π * h) ]
- Slant height s = √(r² + h²)
- Lateral Surface Area L = πrs = πr√(r² + h²)
- Base Surface Area B = πr²
- Total Surface Area A = L + B = πrs + πr²
- If slant height, the lateral surface area of a cone are known, then
- Radius r = L / (π * s)
- Height h = √(s² - r²)
- Base Surface Area B = πr²
- Total Surface Area A = L + B = L + πr²
- If the radius and height of the cone are known, then
- Slant height s = √(r² + h²)
- Volume V = (1/3)πr²h
- Base Surface Area B = πr²
- Lateral Surface Area L = πrs = πr√(r² + h²)
- Total Surface Area A = L + B = πrs + πr² = πr(s + r) = πr(r + √(r² + h²))
Where, r is the cone radius
h is the height
s is the slant height
V is the volume
B is the base surface area
L is the lateral surface area
A is the total surface area of a cone
How to Calculate Cone Surface Area, Slant Height, Volume?
Cone is a solid that has a circular base and a single vertex called the apex. If the vertex is over the center of the base, it is called the right cone. We all know that calculating the measurements of a cone is a little bit difficult when compared with other shapes. Have a look at the detailed step by step procedure that helps solve the cone volume, radius, total surface area, slant height, and height.
Cone Volume:
- Check out the radius, and height of the cone from the question.
- Square the radius and multiply it with π, height.
- Divide the result by 3 to get volume.
Cone Slant Height:
- Get height, the radius of the cone.
- Square the radius and height.
- Add the squared values and apply square root to the result to find slant height.
Cone Radius:
- Process 1:
- Note down slant height, the height of the cone.
- Subtract the square of height from the square of side length.
- Apply square root to the result to find the radius.
- Process 2:
- Check volume, the height of the cone.
- Divide three times of volume by π times height
- Apply square root to the output to get the radius.
- Process 3:
- Get lateral surface area, slant height of the cone.
- Divide the lateral surface area by the product of π and slant height.
Cone Lateral Surface Area:
- Make a note of the cone slant height, radius.
- Get the product of π, radius, and slant height to get the lateral surface area.
Cone Base Surface Area:
- Get the radius of the cone.
- Square the radius and multiply it with π to check the base surface area.
Cone Height:
- Process 1:
- Check slant height, a radius of the cone from the question.
- Subtract the square of the slant height and square of the radius.
- Apply square root to the obtained value to get the height.
- Process 2:
- Find the volume, radius of the cone.
- Get the product of π and square of the radius.
- Divide three times of volume by the result to check the height.
Cone Total Surface Area:
- Calculate lateral, base surface area for the given values.
- Add those lateral surface area, base surface area to check the total surface area.
Solved Example Questions of Circular Cone
Example 1: Compute the circular cone volume, height, slant height, base surface area, and total surface area. If the cone radius is 5 mm and the lateral surface area is 176 mm³.
Solution:
Given that,
Cone lateral surface area L = 176 mm³
Cone radius r = 5 mm
Slant height formula is s = L / (πr)
s = 176 / (π * 5)
= 176 / (3.14 * 5)
= 176 / 15.7 = 11.21 mm
Height h = √(s² - r²)
h = √((11.21)² - 5²)
= √(125.664 - 25) = √(100.664)
= 10.03 mm
Volume V = (1/3)πr²h
V = (1/3) * π * 5² * 10.03
= (1/3) * 3.14 * 25 * 10.03
= 787.35 / 3 = 262.45 mm³
Base Surface Area B = πr²
B = π * 5²
= 3.14 * 25 = 78.5 mm²
Total Surface Area A = L + πr²
A = 176 + 78.5 = 254.5 mm³
∴ Circular cone radius is 5 mm, height is 10.03 mm, slant height is 11.21 mm, volume is 262.45 mm³, lateral surface area is 176 mm³, base surface area is 78.5 mm², and total surface area is 254.5 mm³.
Example 2: A circular cone has a radius of 12 cm, and the height is 18 cm. Find cone lateral surface area, base surface area, total surface area, volume, and slant height?
Solution:
Given that,
The radius of the cone r = 12 cm
Height h = 18 cm
Lateral Surface Area L = πr√(r² + h²)
L = π * 12√(12² + 18²)
= π * 12√(144 + 324)
= π * 12√(468) = 3.14 * 12 * 21.63
= 815.14 cm³
Base Surface Area B = πr²
= π * 12² = π * 144
= 3.14 * 144 = 452.16 cm²
Total Surface Area A = L + B
= 452.16 + 815.14
= 1,267.3 cm³
Slant Height Volume s = √(r² + h²)
s = √(12² + 18²)
= √(144 + 324)
= √(468) = 21.63 cm²
Volume V = (1/3)πr²h
V = (1/3) * π* 12² * 18
= (1/3) * π* 144 * 18
= (1/3) * π* 2592 = (2592π/3)
= 864 π = 864 * 3.14
= 2,712.96 cm³
∴ Circular cone radius is 12 mm, slant height is 21.63 cm², height is 18 cm, volume is 2,712.96 cm³, lateral surface area is 815.14 cm³, base surface area is 452.16 cm², and total surface area is 1,267.3 cm³.
Our website Areavolumecalculator.com provides free calculator tools for you to assist you while solving difficult geometry related problems or to cross-check any concept after your class.
Frequently Asked Questions on Cone Calculator
1. How do you find the volume of a right circular cone?
The formula to calculate the volume of a right circular cone is (1/3)πr²h. Substitute the radius, and height values in this formula and do calculations to get the result.
2. How do you find the missing radius of a cone?
There are multiple ways to find the cone missing radius based on the parameters you have. If you know the volume and height of the cone, the radius will be √[ (3 * v) / (π * h) ]. If you have the lateral surface area and slant height, then the radius is L / (π * s), other way is √(s² - h²) where s is the slant height and h is the height.
3. How do you find the weight of a cone?
To get the cone weight, you must know radius, height, and mean density. The Cone weight formula is (1/3) * π * r² * h * μD. Here μD is the mean density, r is radius and h is the height.
4. What is the formula for the slant height of the cone?
The slant height is the length of the line that joins the cone circular base and apex. By using the Pythagorean theorem, slant height square is the sum of squares of the radius and height. So, slant height is s = √(r² + h²).
